题目内容
13.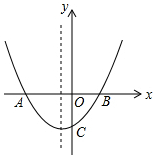 如图抛物线y=ax2+bx+c的图象交x轴于A(-2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
如图抛物线y=ax2+bx+c的图象交x轴于A(-2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:①2b-c=2;②a=$\frac{1}{2}$;③ac=b-1;④$\frac{a+b}{c}$>0
其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据抛物线的开口方向,对称轴公式以及二次函数图象上点的坐标特征来判断a、b、c的符号以及它们之间的数量关系,即可得出结论.
解答 解:据图象可知a>0,c<0,b>0,
∴$\frac{a+b}{c}$<0,故④错误;
∵OB=OC,
∴OB=-c,
∴点B坐标为(-c,0),
∴ac2-bc+c=0,
∴ac-b+1=0,
∴ac=b-1,故③正确;
∵A(-2,0),B(-c,0),抛物线线y=ax2+bx+c与x轴交于A(-2,0)和B(-c,0)两点,
∴2c=$\frac{c}{a}$,
∴2=$\frac{1}{a}$,
∴a=$\frac{1}{2}$,故②正确;
∵ac-b+1=0,
∴b=ac+1,a=$\frac{1}{2}$,
∴b=$\frac{1}{2}$c+1
∴2b-c=2,故①正确;
故选:C.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
1.某宾馆拥有客房90间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入-当日支出)
| x(元) | 200 | 240 | 270 | 300 |
| y(间) | 90 | 70 | 55 | 40 |
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入-当日支出)
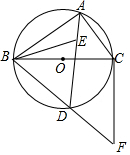 如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
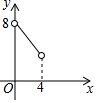
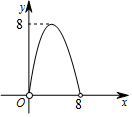
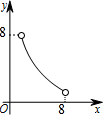
如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.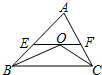 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )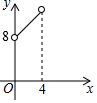
 如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx-6<ax+4<kx的解集为1<x<$\frac{5}{2}$.
如图,直线y=kx和y=ax+4交于A(1,k),则不等式kx-6<ax+4<kx的解集为1<x<$\frac{5}{2}$. 如图,△ABC中,D,E分别是AB,AC的中点,连接DE.若DE=3,则线段BC的长等于6.
如图,△ABC中,D,E分别是AB,AC的中点,连接DE.若DE=3,则线段BC的长等于6.