题目内容
3.如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.(1)如图1,若BD=BA,求证:△ABE≌△DBE;
(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M,求证:①GM=2MC;②AG2=AF•AC.

分析 (1)根据全等三角形的判定定理即可得到结论;
(2)①过G作GH∥AD交BC于H,由AG=BG,得到BH=DH,根据已知条件设DC=1,BD=4,得到BH=DH=2,根据平行线分线段成比例定理得到$\frac{GM}{MC}$=$\frac{HD}{DC}$=$\frac{2}{1}$,求得GM=2MC;
②过C作CN⊥AD交AD的延长线于N,则CN∥AG,根据相似三角形的性质得到$\frac{AG}{NC}$=$\frac{GM}{MC}$,由①知GM=2MC,得到2NC=AG,根据相似三角形的性质得到结论.
解答  证明:(1)在Rt△ABE和Rt△DBE中,$\left\{\begin{array}{l}{BA=BD}\\{BE=BE}\end{array}\right.$,
证明:(1)在Rt△ABE和Rt△DBE中,$\left\{\begin{array}{l}{BA=BD}\\{BE=BE}\end{array}\right.$,
∴△ABE≌△DBE;
(2)①过G作GH∥AD交BC于H,
∵AG=BG,
∴BH=DH,
∵BD=4DC,
设DC=1,BD=4,
∴BH=DH=2,
∵GH∥AD,
∴$\frac{GM}{MC}$=$\frac{HD}{DC}$=$\frac{2}{1}$,
∴GM=2MC;
②过C作CN⊥AC交AD的延长线于N,则CN∥AG,
∴△AGM∽△NCM,
∴$\frac{AG}{NC}$=$\frac{GM}{MC}$,
由①知GM=2MC,
∴2NC=AG,
∵∠BAC=∠AEB=90°,
∴∠ABF=∠CAN=90°-∠BAE,
∴△ACN∽△BAF,
∴$\frac{AF}{CN}$=$\frac{AB}{AC}$,
∵AB=2AG,
∴$\frac{AF}{CN}$=$\frac{2AG}{AC}$,
∴2CN•AG=AF•AC,
∴AG2=AF•AC.
点评 本题考查了相似三角形的,全等三角形的判定和性质,等腰三角形的性质,熟练掌握相似三角形的是解题的关键.

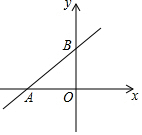 如图,直线y=kx+b与x轴、y轴分别相交于点A(-3,0)、B(0,2),则不等式kx+b>0的解集是( )
如图,直线y=kx+b与x轴、y轴分别相交于点A(-3,0)、B(0,2),则不等式kx+b>0的解集是( )| A. | x>-3 | B. | x<-3 | C. | x>2 | D. | x<2 |
| A. |  | B. |  | C. |  | D. |  |
 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2017次操作后得到的折痕D2016E2016,到BC的距离记为h2017;若h1=1,则h2017的值为2-$\frac{1}{{2}^{2016}}$.
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2017次操作后得到的折痕D2016E2016,到BC的距离记为h2017;若h1=1,则h2017的值为2-$\frac{1}{{2}^{2016}}$.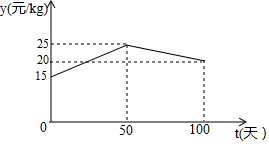 湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).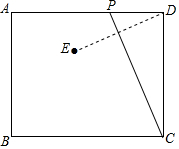 如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).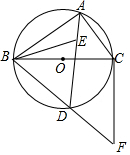 如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.