题目内容
3.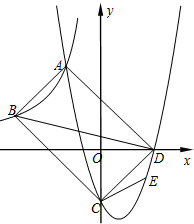 如图,点A(-2,5)和点B(-5,a)在反比例函数y=$\frac{k}{x}$的图象上,直线y=x+b分别交x轴的正半轴于点D,交y轴的负半轴于点C,且AB=CD.二次函数的图象经过A、C、D三点.
如图,点A(-2,5)和点B(-5,a)在反比例函数y=$\frac{k}{x}$的图象上,直线y=x+b分别交x轴的正半轴于点D,交y轴的负半轴于点C,且AB=CD.二次函数的图象经过A、C、D三点.(1)求a、k的值及直线AB的函数表达式;
(2)求点C、D的坐标及二次函数的表达式;
(3)如果点E在第四象限的二次函数图象上,且∠OCE=∠BDC,求点E的坐标.
分析 (1)设反比例函数的解析式为:y=$\frac{k}{x}$由A的坐标可求出k的值,B的横坐标已知,所以可求出纵坐标,设直线AB的表达式为y=mx+n,分别把A,B坐标代入求出m和n的值即可;
(2)由直线CD的表达式为y=x+b,得到点C,D的坐标,根据AB=CD,列出等式即可求出b的值,然后把点A,C,D的坐标代入二次函数的解析式即可求出;
(3)设二次函数的解析式为y=a1x2+b1x-3,由已知条件易求a1和b1的值,作EF⊥y轴,BG⊥y轴,垂足分别为F、G.设CF=3t,则EF=5t,OF=3-3t,代入抛物线的解析式求出t的值即可.
解答 解:(1)∵点A(-2,5)和点B(-5,a)在反比例函数y=$\frac{k}{x}$的图象上,
∴5=$\frac{k}{-2}$,∴k=-10,
∴反比例函数的解析式为:y=$\frac{-10}{x}$,
a=$\frac{-10}{-5}$=2,
∴点B的坐标为(-5,2),
设直线AB的表达式为:y=mx+n,
则$\left\{\begin{array}{l}{5=-2m+n}\\{2=-5m+n}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=1}\\{n=7}\end{array}\right.$,
∴直线AB的表达式为:y=x+7,
(2)在y=x+b中,令x=0,y=b,令y=0,x=-b,
∴C(0,b),D(-b,0)
∵CD=AB,
∴CD2=AB2,
∴b2+b2=(-5+2)2+(2-5)2,
∴b=±3,∵b<0,∴b=-3,
∴点C、D的坐标分别是(0,-3)、(3,0),
设二次函数的解析式为:y=a1x2+b1x-3,
∴$\left\{\begin{array}{l}{5={4a}_{1}-{2b}_{1}-3}\\{0={9a}_{1}+{3b}_{1}-3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{a}_{1}=1}\\{{b}_{1}=-2}\end{array}\right.$,
∴二次函数的解析式为:y=x2-2x-3,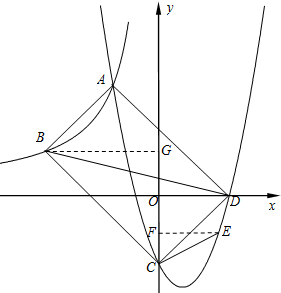
(3)作EF⊥y轴,BG⊥y轴,垂足分别为F、G
∵B(-5,2),C(0,-3),D(3,0),
∴OC=OD,BG=CG,
∴∠BCG=∠OCD=45°,
∴∠BCD=90°,
∵∠OCE=∠BDC,
∴tan∠OCE=tan∠BDC=$\frac{BC}{CD}$=$\frac{5\sqrt{2}}{3\sqrt{2}}$=$\frac{5}{3}$,
设CF=3t,则EF=5t,OF=3-3t
∴点E(5t,3t-3)…(11分)
∴3t-3=25t2-10t-3,
∴t1=0,t2=$\frac{13}{25}$,
∴点E($\frac{13}{5}$,-$\frac{36}{25}$).
点评 此题考查了待定系数法求反比例函数、一次函数、二次函数的解析式、直角三角形的判定和性质、平行四边形的判定和性质、等腰三角形的判定和性质以及锐角三角形的运用和两点间的距离公式的运用.此题难度较大,注意掌握方程思想与数形结合思想的应用.

 阅读快车系列答案
阅读快车系列答案| A. | 圆A与圆B外离 | B. | 圆B与圆C外离 | C. | 圆A与圆C外离 | D. | 圆A与圆B相交 |
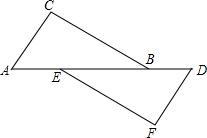 如图,已知AE=DB,BC=EF,BC∥EF,求证:△ABC≌△DEF.
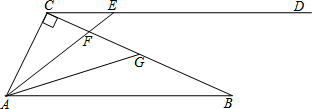
如图,已知AE=DB,BC=EF,BC∥EF,求证:△ABC≌△DEF.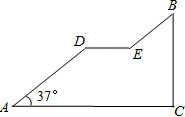 如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.
如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.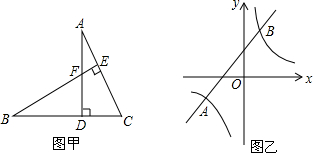
 已知:如图,点D,E分别在AC,AB上,且∠B=∠C.求证:
已知:如图,点D,E分别在AC,AB上,且∠B=∠C.求证: