题目内容
13．先化简，再求值：（$\frac{3x}{x-2}$-$\frac{x}{x+2}$）÷$\frac{2x}{{x}^{2}-4}$，其中x是小于3的非负整数．分析 先根据分式混合运算的法则把原式进行化简，再根据x是小于3的非负整数选取合适的x的值，代入进行计算即可．
解答 解：原式=$\frac{3x（x+2）-x（x-2）}{（x-2）（x+2）}$•$\frac{（x+2）（x-2）}{2x}$
=$\frac{3{x}^{2}+6x-{x}^{2}+2x}{（x-2）（x+2）}$•$\frac{（x+2）（x-2）}{2x}$
=$\frac{2x（x+4）}{（x-2）（x+2）}$•$\frac{（x+2）（x-2）}{2x}$
=x+4．
∵x是小于3的非负整数，
∴x=0，1，2，
∵x=0，2时分式无意义，
∴x=1，
∴原式=1+4=5．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
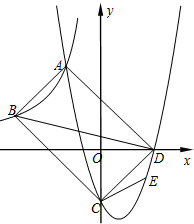如图，点A（-2，5）和点B（-5，a）在反比例函数y=$\frac{k}{x}$的图象上，直线y=x+b分别交x轴的正半轴于点D，交y轴的负半轴于点C，且AB=CD．二次函数的图象经过A、C、D三点．
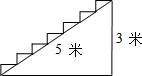如图所示，在高为3m，斜坡长为5m的楼梯表面铺地毯，至少需要地毯7米．
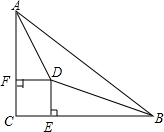如图所示△ABC中，∠C=90°，∠A，∠B的平分线交于D点，DE⊥BC于点E，DF⊥AC于点F．