题目内容
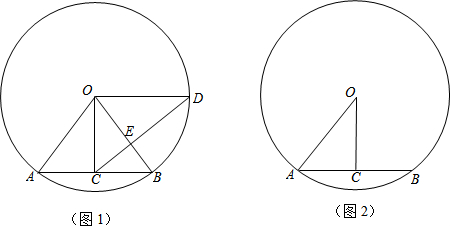
14.如图,在Rt△ABC中,∠ACB=90°.AB=13,CD∥AB.点E为射线CD上一动点(不与点C重合),联结AE,交边BC于点F,∠BAE的平分线交BC于点G.(1)当时CE=3,求S△CEF:S△CAF的值;
(2)设CE=x,AE=y,当CG=2GB时,求y与x之间的函数关系式;
(3)当AC=5时,联结EG,若△AEG为直角三角形,求BG的长.
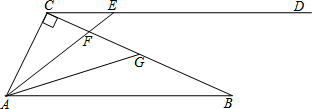
分析 (1)过点C作CH⊥AE于H,根据等高的两个三角形面积之比等于底的比,求出EF:AF即可;
(2)延长AG交射线CD于点K,根据相似三角形对应边成比例求出y与x之间的函数关系式;
(3)分∠AGE=90°、∠AEG=90°两种情况进行解答,求出BG的长.
解答 解:(1)过点C作CH⊥AE于H,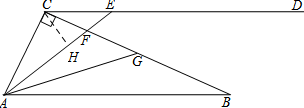
∴$\frac{{S}_{△CEF}}{{S}_{△CAF}}$=$\frac{\frac{1}{2}EF•CH}{\frac{1}{2}AF•CH}$=$\frac{EF}{AF}$,
∵CD∥AB,∴$\frac{EF}{AF}=\frac{CE}{AB}$,
∵CE=3,AB=13,∴$\frac{EF}{AF}$=$\frac{3}{13}$,
∴$\frac{{S}_{△CEF}}{{S}_{△CAF}}$=$\frac{3}{13}$.
(2)延长AG交射线CD于点K,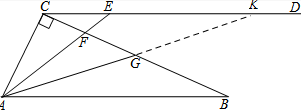
∵CD∥AB,
∴∠EKA=∠KAB,
∵AG平分∠BAE,
∴∠EAK=∠KAB,
∴∠EKA=∠EAK,
∴AE=EK,
∵CE=x,AE=y,
∴CK=CE+EK=CE+AE=x+y,
∵CD∥AB,
∴$\frac{CK}{AB}$=$\frac{CG}{GB}$,
∵CG=2GB,
∴$\frac{CK}{AB}$=2,
∴$\frac{x+y}{13}=2$,
∴y=26-x.
(3)由题意,得:BC=12,
①当∠AGE=90°时,则AG=GK,
∵CD∥AB,
∴BG=$\frac{1}{2}$BC=6.
②当∠AEG=90°时,则△ACF∽△GEF,
∴$\frac{CF}{AF}$=$\frac{EF}{FG}$,∠CFE=∠AFG,
∴△ECF∽△GAF,
∴∠ECF=∠FAG,
又∵∠FAG=∠GAB,∠ECF=∠B,
∴∠B=∠GAB,∴GA=GB,
过点G作GN⊥AB于N,∴BN=$\frac{1}{2}$AB=$\frac{13}{2}$,
∴BG=$\frac{13}{12}$BN=$\frac{169}{24}$.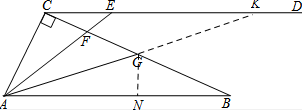
点评 本题考查的是相似三角形的综合应用,灵活运用相似三角形的判定定理和性质定理是解题的关键,本题可以提高学生综合运用知识的能力、逻辑思维能力.

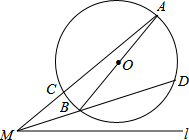 如图,AB为⊙O的直径,M为⊙O外一点,连接MA与⊙O交于点C,连接MB并延长交⊙O于点D,经过点M的直线l与MA所在直线关于直线MD对称,作BE⊥l于点E,连接AD,DE
如图,AB为⊙O的直径,M为⊙O外一点,连接MA与⊙O交于点C,连接MB并延长交⊙O于点D,经过点M的直线l与MA所在直线关于直线MD对称,作BE⊥l于点E,连接AD,DE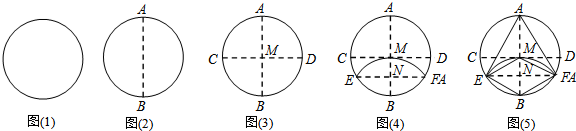
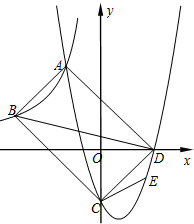 如图,点A(-2,5)和点B(-5,a)在反比例函数y=$\frac{k}{x}$的图象上,直线y=x+b分别交x轴的正半轴于点D,交y轴的负半轴于点C,且AB=CD.二次函数的图象经过A、C、D三点.
如图,点A(-2,5)和点B(-5,a)在反比例函数y=$\frac{k}{x}$的图象上,直线y=x+b分别交x轴的正半轴于点D,交y轴的负半轴于点C,且AB=CD.二次函数的图象经过A、C、D三点.