题目内容
15.(1)如图甲,AD丄BC于点D,BE丄AC于点E,AD与BE相交于点F,且BF=AC.求证:DF=DC.(2)如图乙,已知一次函数与反比例函数的图象交于点A(-4,一2)和B(a,4)
①求反比例函数的解析式和点B的坐标;
②根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
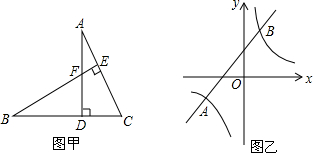
分析 (1)根据角平分线的性质就可以得出CE=CF,再由HL证明△CEB≌△CFD就可以得出结论.
(2)①设反比例函数解析式为y=$\frac{k}{x}$,把点A的坐标代入解析式,利用待定系数法求反比例函数解析式即可,把点B的坐标代入反比例函数解析式进行计算求出a的值,从而得到点B的坐标;②写出一次函数图象在反比例函数图象上方的x的取值范围即可.
解答 解(1)证明:AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=BEC=90°,
在△BDF与△ADC中,$\left\{\begin{array}{l}{∠BDF=∠ADC}\\{∠B=∠A}\\{BF=AC}\end{array}\right.$,
∴△BDF≌△ADC,
∴DF=DC;
(2)①设反比例函数的解析式为y=$\frac{k}{x}$(k≠0),
∵反比例函数图象经过点A(-4,-2),
∴-2=$\frac{k}{-4}$,
∴k=8,
∴反比例函数的解析式为y=$\frac{8}{x}$,
∵B(a,4)在y=$\frac{8}{x}$的图象上,
∴4=$\frac{8}{a}$,
∴a=2,
∴点B的坐标为B(2,4);
②根据图象得,当x>2或-4<x<0时,一次函数的值大于反比例函数的值.
点评 本题考查了角平分线的性质的运用,全等三角形的判定与性质的运用,解答时证明△CEB≌△CFD是关键反比例函数与一次函数的交点问题,根据点A的坐标求出反比例函数解析式是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
10.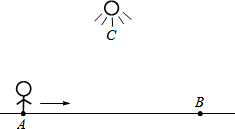 我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
 我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )| A. | y=x? | B. | y=x+3 | C. | y=$\frac{3}{x}$? | D. | y=(x-3)2+3 |
7.任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
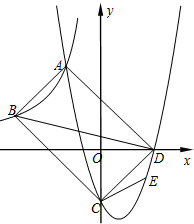 如图,点A(-2,5)和点B(-5,a)在反比例函数y=$\frac{k}{x}$的图象上,直线y=x+b分别交x轴的正半轴于点D,交y轴的负半轴于点C,且AB=CD.二次函数的图象经过A、C、D三点.
如图,点A(-2,5)和点B(-5,a)在反比例函数y=$\frac{k}{x}$的图象上,直线y=x+b分别交x轴的正半轴于点D,交y轴的负半轴于点C,且AB=CD.二次函数的图象经过A、C、D三点.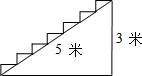 如图所示,在高为3m,斜坡长为5m的楼梯表面铺地毯,至少需要地毯7米.
如图所示,在高为3m,斜坡长为5m的楼梯表面铺地毯,至少需要地毯7米.