题目内容
8.在半径为2的圆中,弦AB的长为2,则$\widehat{AB}$长等于$\frac{2}{3}$π.分析 连接OA、OB,求出圆心角∠AOB的度数,代入弧长公式求出即可.
解答  解:连接OA、OB,
解:连接OA、OB,
∵OA=OB=AB=2,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴$\widehat{AB}$的长为:$\frac{60π×2}{180}$=$\frac{2}{3}π$,
故答案为:$\frac{2}{3}$π.
点评 本题考查了弧长公式,等边三角形的性质和判定的应用,注意:已知圆的半径是R,弧AB对的圆心角的度数是n°,则弧AB的长=$\frac{nπr}{180}$.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
16.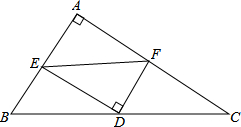 如图,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若BE=2,CF=3,则EF的值可能为( )
如图,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若BE=2,CF=3,则EF的值可能为( )
 如图,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若BE=2,CF=3,则EF的值可能为( )
如图,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若BE=2,CF=3,则EF的值可能为( )| A. | 7 | B. | 6 | C. | 5 | D. | $\sqrt{13}$ |
17.一元二次方程x2+x+$\frac{1}{4}$=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
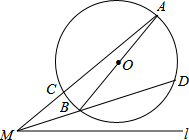 如图,AB为⊙O的直径,M为⊙O外一点,连接MA与⊙O交于点C,连接MB并延长交⊙O于点D,经过点M的直线l与MA所在直线关于直线MD对称,作BE⊥l于点E,连接AD,DE
如图,AB为⊙O的直径,M为⊙O外一点,连接MA与⊙O交于点C,连接MB并延长交⊙O于点D,经过点M的直线l与MA所在直线关于直线MD对称,作BE⊥l于点E,连接AD,DE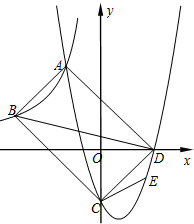 如图,点A(-2,5)和点B(-5,a)在反比例函数y=$\frac{k}{x}$的图象上,直线y=x+b分别交x轴的正半轴于点D,交y轴的负半轴于点C,且AB=CD.二次函数的图象经过A、C、D三点.
如图,点A(-2,5)和点B(-5,a)在反比例函数y=$\frac{k}{x}$的图象上,直线y=x+b分别交x轴的正半轴于点D,交y轴的负半轴于点C,且AB=CD.二次函数的图象经过A、C、D三点.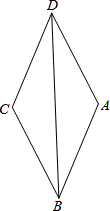 如图,四边形ABCD是菱形,对角线BD上有一点O,以O为圆心,OD长为半径的圆记为⊙O.
如图,四边形ABCD是菱形,对角线BD上有一点O,以O为圆心,OD长为半径的圆记为⊙O.