题目内容
18.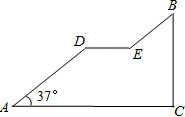 如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.
如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
分析 首先延长BE交AC于点F,再利用锐角三角函数关系得出FC的长,进而求出DE的长.
解答  解:延长BE交AC于点F
解:延长BE交AC于点F
∵AD∥BE,
∴∠BFC=∠A=37°,
又∵BC⊥AC,即∠C=90°,
∴tan∠BFC=$\frac{BC}{FC}$,
∴FC=$\frac{BC}{tan∠BFC}$=$\frac{4.8}{tan37°}$≈$\frac{4.8}{0.75}$≈6.4(m),
∴AF=AC-FC=8-6.4=1.6(米),
∵AD∥BE,DE∥AC,
∵四边形ADEF是平行四边形,
∴DE=AF=1.6米.
点评 此题主要考查了解直角三角形的应用,得出FC的长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.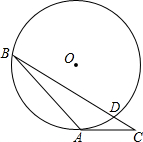 在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是( )
在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是( )
 在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是( )
在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是( )| A. | 1 | B. | 3 | C. | $\sqrt{3}$ | D. | 2 |
10.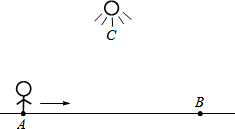 我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
 我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )| A. | y=x? | B. | y=x+3 | C. | y=$\frac{3}{x}$? | D. | y=(x-3)2+3 |
7.任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
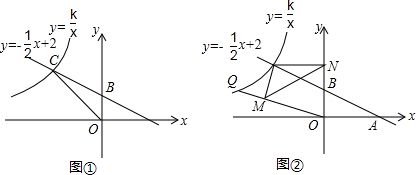
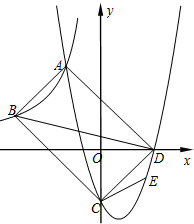 如图,点A(-2,5)和点B(-5,a)在反比例函数y=$\frac{k}{x}$的图象上,直线y=x+b分别交x轴的正半轴于点D,交y轴的负半轴于点C,且AB=CD.二次函数的图象经过A、C、D三点.
如图,点A(-2,5)和点B(-5,a)在反比例函数y=$\frac{k}{x}$的图象上,直线y=x+b分别交x轴的正半轴于点D,交y轴的负半轴于点C,且AB=CD.二次函数的图象经过A、C、D三点.