题目内容
12.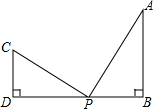 如图:若AB⊥BD,CD⊥BD,动点P在BD上且CP⊥AP,若AB=3,CD=2,BD=7.
如图:若AB⊥BD,CD⊥BD,动点P在BD上且CP⊥AP,若AB=3,CD=2,BD=7.(1)说明:△ABP∽△PDC;
(2)求出DP的长.
分析 (1)欲证明△ABP∽△PDC,只要证明∠APB=∠C,∠B=∠D=90°即可.
(2)设DP=x,利用相似三角形的性质,列出方程即可解决问题.
解答 (1)证明:∵AB⊥BD,CD⊥BD,CP⊥AP,
∴∠D=∠B=∠CPA=90°,
∴∠C+∠CPD=90°,∠CPD+∠APB=90°,
∴∠C=∠APB,
∴△ABP∽△PDC.
(2)设DP=x,
∵△ABP∽△PDC,
∴$\frac{AB}{PD}$=$\frac{PB}{CD}$,
∴$\frac{3}{x}$=$\frac{7-x}{2}$,
解得x=1或6,
经检验x=1或6都是用方程的解.
∴DP=1或6.
点评 本题考查相似三角形的判定和性质、等角的余角相等等知识,解题的关键是熟练应用相似三角形的判定证明两个三角形相似,学会利用参数,把问题转化为方程去思考,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

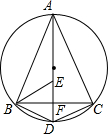 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD. 尺规作图:已知∠α,求作:∠A使∠A=∠α( 不写作法,保留痕迹 )
尺规作图:已知∠α,求作:∠A使∠A=∠α( 不写作法,保留痕迹 )