题目内容
17.已知关于x的方程x2-(2k+1)x+4(k-$\frac{1}{2}$)=0(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的底边长为a=3,两腰的长b、c恰好是这个方程的两个根,求△ABC的周长.
分析 (1)根据方程各项的系数利用根的判别式即可得出△=(2k-3)2≥0,此题得证;
(2)根据等腰三角形的性质即可得出k的值,将其代入方程求出b、c的值,再根据三角形的周长公式即可得出结论.
解答 (1)证明:在方程x2-(2k+1)x+4(k-$\frac{1}{2}$)=0中,
△=[-(2k+1)]2-4×1×4(k-$\frac{1}{2}$)=(2k-3)2≥0,
∴不论k取什么实数值,这个方程总有实数根;
(2)解:∵三角形为等腰三角形,
∴△=(2k-3)2=0,
∴k=$\frac{3}{2}$.
将k=$\frac{3}{2}$代入原方程中,得:x2-4x+4=0,
解得:b=c=2,
∴C△ABC=A+B+C=7.
点评 本题考查了根的判别式以及等腰三角形的性质,根据方程根的判别式的符号确定方程解得情况是解题的关键.

练习册系列答案
相关题目
7.某班七年级第二学期数学一共进行四次考试,小丽和小明的成绩如表所示:
(1)请你通过计算这四次考试成绩的方差,比较谁的成绩比较稳定?
(2)若老师计算学生的学期总评成绩按照如下的标准:单元测验1占10%,单元测验2占10%,期中考试占30%,期末考试占50%.请你通过计算,比较谁的学期总评成绩高?
| 学生 | 单元测验1 | 期中考试 | 单元测验2 | 期未考试 |
| 小丽 | 80 | 70 | 90 | 80 |
| 小明 | 60 | 90 | 80 | 90 |
(2)若老师计算学生的学期总评成绩按照如下的标准:单元测验1占10%,单元测验2占10%,期中考试占30%,期末考试占50%.请你通过计算,比较谁的学期总评成绩高?
 如图,这是一个供滑板爱好者滑行使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=8m,点E在CD上,CE=2m,一位滑行爱好者从A点到E点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取3)
如图,这是一个供滑板爱好者滑行使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=8m,点E在CD上,CE=2m,一位滑行爱好者从A点到E点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取3)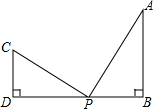 如图:若AB⊥BD,CD⊥BD,动点P在BD上且CP⊥AP,若AB=3,CD=2,BD=7.
如图:若AB⊥BD,CD⊥BD,动点P在BD上且CP⊥AP,若AB=3,CD=2,BD=7.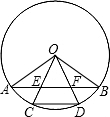 如图,OA、OB是⊙O的两条半径,且OA⊥OB,C、D是$\widehat{AB}$的三等两点,OC、OD分别交AB于E、F,则AE、CD与BF相等吗?为什么?
如图,OA、OB是⊙O的两条半径,且OA⊥OB,C、D是$\widehat{AB}$的三等两点,OC、OD分别交AB于E、F,则AE、CD与BF相等吗?为什么? 如图,化简:|a|-|a+b|+|c-a|+|b+c|
如图,化简:|a|-|a+b|+|c-a|+|b+c|