题目内容
4.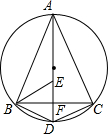 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.(1)求证:BD=DE;
(2)请判断E,C两点是否在以D为圆心,DB为半径的圆上,并说明理由.
分析 (1)利用等弧对等弦即可证明.
(2)利用等弧所对的圆周角相等,可得∠BAD=∠CBD,再等量代换得出∠DBE=∠DEB,从而证明DB=DE=DC,所以E,C两点在以D为圆心,DB为半径的圆上.
解答 (1)证明:∵AD为直径,AD⊥BC,
∴$\widehat{BD}$=$\widehat{CD}$,
∴BD=CD.
(2)B,E,C三点在以D为圆心,以DB为半径的圆上.
理由:由(1)知:$\widehat{BD}$=$\widehat{CD}$,
∴∠BAD=∠CBD,
又∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠ABE,∠CBE=∠ABE,
∴∠DBE=∠DEB,
∴DB=DE.
由(1)知:BD=CD,
∴DB=DE=DC.
∴E,C两点在以D为圆心,以DB为半径的圆上.
点评 本题主要考查等弧对等弦,及确定一个圆的条件,此类题是中考的常考题,需要同学们牢固掌握.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
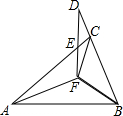 如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25.
如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25.
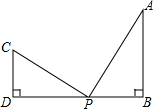 如图:若AB⊥BD,CD⊥BD,动点P在BD上且CP⊥AP,若AB=3,CD=2,BD=7.
如图:若AB⊥BD,CD⊥BD,动点P在BD上且CP⊥AP,若AB=3,CD=2,BD=7. 已知:如图,直线AB,CD被直线EF所截,AB∥CD,交点分别为G、H,射线GM平分∠EGB,射线HN平分∠EHD.
已知:如图,直线AB,CD被直线EF所截,AB∥CD,交点分别为G、H,射线GM平分∠EGB,射线HN平分∠EHD. 已知AB∥CD,图形中∠AEC与∠A、∠C有怎样的数量关系?并说明理由.
已知AB∥CD,图形中∠AEC与∠A、∠C有怎样的数量关系?并说明理由.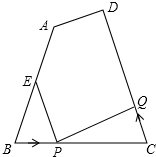 如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.