��Ŀ����
13������Լ�֣���$\frac{x}{3{x}^{2}}$=$\frac{1}{3x}$����$\frac{a+m}{b+m}$=$\frac{a}{b}$����$\frac{2}{2+a}$=$\frac{1}{1+a}$����$\frac{2+xy}{xy+2}$=1����$\frac{{a}^{2}-1}{a+1}$=a-1����$\frac{-��x-y��}{��x-y��^{2}}$=-$\frac{1}{x-y}$��������ȷ���У�������| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
���� ���ݷ�ʽ�ķ��ӷ�ĸ�����Ի����ͬһ����Ϊ�����ʽ����ʽ��ֵ���䣬�ɵô𰸣�
��� �⣺��$\frac{x}{3{x}^{2}}$=$\frac{1}{3x}$���ӷ�ĸ������x���ʢ���ȷ��
��$\frac{a+m}{b+m}$=$\frac{a}{b}$���ӷ�ĸ����m���ʢڴ���
��$\frac{2}{2+a}$=$\frac{1}{1+a}$���ӷ�ĸ����1���ʢ۴���
��$\frac{2+xy}{xy+2}$=1���ӷ�ĸ�����ԣ�xy+2�����ʢ���ȷ��
��$\frac{{a}^{2}-1}{a+1}$=a-1���ӷ�ĸ�����ԣ�a+1�����ʢ���ȷ��
��$\frac{-��x-y��}{��x-y��^{2}}$=-$\frac{1}{x-y}$���ӷ�ĸ�����ԣ�x-y�����ʢ���ȷ��
��ѡ��C��
���� ���⿼���˷�ʽ�������ʣ���ʽ�ķ��ӷ�ĸ�����Ի����ͬһ����Ϊ�����ʽ����ʽ��ֵ���䣬��ע��ʽ�ķ��ӷ�ĸ���ӻ��ͬһ��������ʽ��ֵ�����仯��

��ϰ��ϵ�д�
 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
�����Ŀ
5��С��Ϊ�о�����������y=$\frac{2}{x}$��ͼ����-2��-1��1������ȡһ����Ϊ�����꣬��-1��2������ȡһ����Ϊ��������ɵ�P�����꣬��P�ڷ���������y=$\frac{2}{x}$��ͼ���ϵĸ����ǣ�������
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
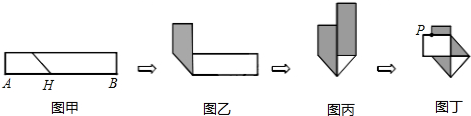
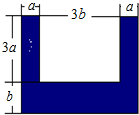 ��ͼ��
��ͼ��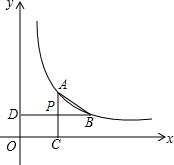 ��ͼ����֪��A��B��˫����y=$\frac{k}{x}$ ��x��0���ϣ�AC��x����C��BD��y���ڵ�D��AC��BD���ڵ�P��P��AC���е㣮
��ͼ����֪��A��B��˫����y=$\frac{k}{x}$ ��x��0���ϣ�AC��x����C��BD��y���ڵ�D��AC��BD���ڵ�P��P��AC���е㣮