题目内容
2.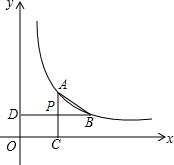 如图,已知点A、B在双曲线y=$\frac{k}{x}$ (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
如图,已知点A、B在双曲线y=$\frac{k}{x}$ (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.(1)设A的横坐标为m,试用m、k表示B的坐标.
(2)试判断四边形ABCD的形状,并说明理由.
(3)若△ABP的面积为3,求该双曲线的解析式.
分析 (1)根据点P是AC的中点得到点A的横坐标是m,结合反比例函数图象上点的坐标特征来求点B的坐标;
(2)根据点P的坐标得到点P是BD的中点,所以由“对角线互相垂直平分的四边形是菱形”得到四边形ABCD是菱形;
(3)由△ABP的面积为3,知BP•AP=6.根据反比例函数 y=kx中k的几何意义,知本题k=OC•AC,由反比例函数的性质,结合已知条件P是AC的中点,得出OC=BP,AC=2AP,进而求出k的值.
解答 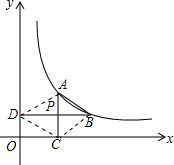 解:(1)∵A的横坐标为m,AC⊥x轴于C,P是AC的中点,
解:(1)∵A的横坐标为m,AC⊥x轴于C,P是AC的中点,
∴点B的横坐标是2m.
又∵点B在双曲线y=$\frac{k}{x}$ (x>0)上,
∴B(2m,$\frac{k}{2m}$).
(2)连接AD、CD、BC;
∵AC⊥x轴于C,BD⊥y轴于点D,
∴AC⊥BD;
∵A(m,$\frac{k}{m}$),B(2m,$\frac{k}{2m}$),
∴P(m,$\frac{k}{2m}$),
∴PD=PB,
又AP=PC,
∴四边形ABCD是菱形;
(3)∵△ABP的面积为 $\frac{1}{2}$•BP•AP=3,
∴BP•AP=6,
∵P是AC的中点,
∴A点的纵坐标是B点纵坐标的2倍,
又∵点A、B都在双曲线y=$\frac{k}{x}$(x>0)上,
∴B点的横坐标是A点横坐标的2倍,
∴OC=DP=BP,
∴k=OC•AC=BP•2AP=12.
∴该双曲线的解析式是:y=$\frac{12}{x}$
点评 主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
17.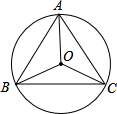 如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )
如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )
 如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )
如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )| A. | 60° | B. | 150° | C. | 180° | D. | 240° |
7.一组数据4,3,6,9,6,5的极差和众数分别是( )
| A. | 5和5.5 | B. | 5.5和6 | C. | 5和6 | D. | 6和6 |
11.下列运算中,结果正确的是( )
| A. | a3+a4=a7 | B. | 3a2+a2=4a4 | C. | 3a-2a=a | D. | 4a2-a2=4 |
12.某儿童服装店老板以25元的价格买进30件连衣裙,针对不同的顾客,连衣裙的售价不完全相同,若以45元为标准,将超过的钱数记为正,不足的钱数记为负,则记录结果如下表所示:
问该服装店在售完这30件连衣裙后,赚了多少钱?
| 售出件数 | 7 | 6 | 3 | 5 | 4 | 5 |
| 售价/元 | +3 | +2 | +1 | 0 | -1 | -1 |