题目内容

1．用16m长的篱笆围成长方形的生物园来饲养动物，则最大面积16m2．

分析 设该长方形生物园的长为x，面积为y，则该生物园的宽为8-x，则可列出函数关系式y=x（8-x），然后求最大值即可．

解答 解：设该长方形生物园的长为x，面积为y，则该生物园的宽为8-x，
则可得：0＜x＜8，
根据题意列出函数关系式得：y=x（8-x）=-x2+8x=-（x-4）2+16，
∵-1＜0，
∴开口向下，y有最大值，
故当x=4时，y取最大值16．
即围成的最大面积是16m2．
故答案为：16m2．

点评 本题考查了二次函数的应用，解答本题的关键是设出矩形的长，表示出宽，得出面积S关于x的函数表达式，注意配方法求二次函数最值得应用．

练习册系列答案
相关题目
1．若△ABC的三边长满足（AC+AB）（AC-AB）-BC2=0，则下列结论正确的是（　　）
A．△ABC是直角三角形，且∠C=90°B．△ABC是直角三角形，且∠A=90°
C．△ABC是直角三角形，且∠B=90°D．△ABC不是直角三角形
2．在数轴上与原点距离为$\frac{1}{3}$个单位长度的点表示的数是$\frac{1}{3}$或$-\frac{1}{3}$，在数轴上与表示2的点距离为5个单位长度的点表示的数为7或-3．
9．如图，直线l与⊙O相切于点C，A、B、D均在⊙O上，OA∥l，∠BDC=85°，则∠BAO的度数为50°．
16．如图，将矩形ABCD置于平面直角坐标系中，其中AD边在x轴上，AB=2，直线MN：y=x-4沿x轴的负方向以每秒1个单位的长度平移，设在平移过程中该直线被矩形ABCD的边截得的线段长度为m，平移时间为t，m与t的函数图象如图2所示．
（1）点A的坐标为（1，0），矩形ABCD的面积为8；
（2）求a，b的值；
（3）在平移过程中，求直线MN扫过矩形ABCD的面积S与t的函数关系式，并写出自变量t的取值范围．
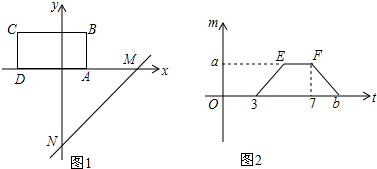
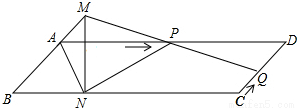6．已知：如图，?ABCD中，AD=3cm，CD=1cm，∠B=45°，点P从点A出发，沿AD方向匀速运动，速度为3cm/s；点Q从点C出发，沿CD方向匀速运动，速度为1cm/s，连接并延长QP交BA的延长线于点M，过M作MN⊥BC，垂足是N，设运动时间为t（s）（0＜t＜1）
解答下列问题：
（1）填空：AM=tMN=$\frac{\sqrt{2}}{2}（t+1）$（用t表示）；
（2）若四边形ANPM的面积为$\frac{9\sqrt{2}}{16}$cm2，求t的值；
（3）在（2）的条件下判断四边形MAQD的形状，并说明理由；
（4）连接AC交NP于点O，是否存在某一时刻t，使AO：OC=$\sqrt{2}$：1？若存在，求出相应的t值；若不存在，说明理由．
13．下列约分：①$\frac{x}{3{x}^{2}}$=$\frac{1}{3x}$；②$\frac{a+m}{b+m}$=$\frac{a}{b}$；③$\frac{2}{2+a}$=$\frac{1}{1+a}$；④$\frac{2+xy}{xy+2}$=1；⑤$\frac{{a}^{2}-1}{a+1}$=a-1；⑥$\frac{-（x-y）}{（x-y）^{2}}$=-$\frac{1}{x-y}$，其中正确的有（　　）
A．2个B．3个C．4个D．5个
10．反比例函数为y=$\frac{4}{x}$，则当函数值y≤-2时，自变量x的取值范围是-2≤x＜0．
11．下列运算中，结果正确的是（　　）
A．a3+a4=a7B．3a2+a2=4a4C．3a-2a=aD．4a2-a2=4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网