题目内容
4. 如图,△ABC中,∠ACB=30°,CD⊥AB于D,E为CD上一点,使得∠CAE=30°,连接BE,求证:∠BED=3∠BCD.
如图,△ABC中,∠ACB=30°,CD⊥AB于D,E为CD上一点,使得∠CAE=30°,连接BE,求证:∠BED=3∠BCD.
分析 以AC为边向下作等边三角形△ACG,以BG为边向右作等边三角形△BGI,连接EB,EI,先证明△AGB≌△CGI,根据等腰三角形三线合一的性质得到AB=BG=IG=IC,EG=EC可以证明,∠BEG=∠IEG=∠CEI,再由∠BEG=∠IEG=∠CEI=60°-∠2和∠DEB=180°-3∠CEI得到证明.
解答 证明:如图以AC为边向下作等边三角形△ACG,以BG为边向右作等边三角形△BGI,连接EB,EI.
∵∠BGI=∠AGC=60°,
∴∠BGA=∠CGI,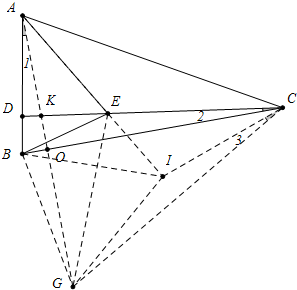
在△ACG和△CGI中,
$\left\{\begin{array}{l}{AG=CG}\\{∠AGB=∠CGI}\\{BG=GI}\end{array}\right.$,
∴△AGB≌△CGI,
∴∠1=∠3,∵CA=CG,∠ACB=∠BCG=30°,
∴BC⊥AG,AO=OG,
∴BC垂直平分AG,
∴BA=BG,
∴AB=BG=GI=IC,
∵AG=AC,∠EAI=∠EAC=30°,
∴AE垂直平分GC,
∵IG=IC,
∴点I在CG的垂直平分线上,
∴A、E、I共线,
∴EG=EC,∠GEI=∠CEI,
∵∠1+∠DKA=90°,∠2+∠OKC=90°,∠DKA=∠OKC,
∴∠1=∠2=∠3,
∴∠ECI=∠BCG=30°,
∵∠EGC=∠ECG,∠IGC=∠ICG,
∴∠EGI=∠ECI=30°,
∵∠BGI=60°,
∴∠BGE=∠IGE=30°,
∵BG=GI,
∴GE垂直平分BI,
∴EB=EI,∠BEG=∠IEG=∠CEI,
∵∠CEI=∠EAC+∠ACE,
∴∠CEI+∠2=∠EAC+∠ACE+∠2=60°,
∴∠BEG=∠IEG=∠CEI=60°-∠2,
∵∠DEB=180°-3∠CEI=180°-3(60°-∠2)=3∠2,
即∠BED=3∠DCB.
点评 本题考查等边三角形的性质、线段垂直平分线的判定和性质,添加辅助线构造两个等边三角形是解决问题的关键.

| A. | 需要证明的命题 | B. | 公理 | C. | 定理 | D. | 定义 |
 如图所示,请找出图中所有的互为同旁内角的角.
如图所示,请找出图中所有的互为同旁内角的角. 如图,在△ABC中,点D是BC的中点,FD⊥ED,延长ED到点P.使ED=PD,连结FP与CP,试判断BE+CF与EF的大小关系.
如图,在△ABC中,点D是BC的中点,FD⊥ED,延长ED到点P.使ED=PD,连结FP与CP,试判断BE+CF与EF的大小关系. A、B两村之间隔一条河,现在要在河上架一座桥.
A、B两村之间隔一条河,现在要在河上架一座桥.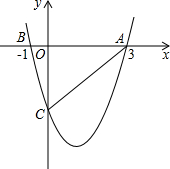 如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.
如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.