Question

9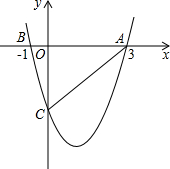．如图，二次函数y=$\frac{4}{3}$x²+bx+c的图象与x轴交于A（3，0），B（-1，0），与y轴交于点C．
（1）写出该二次函数的表达式及点C的坐标；
（2）在线段AC下方的抛物线上是否存在点N，使△ACN与三角形△ABC的面积比为1：2？若存在请求出N的坐标，若不存在请说明理由；
（3）作以AB为直径的⊙M，交y轴于E点，过点E且与⊙M相切的直线1交x轴于F点．求直线1的函数表达式．

Answer 1

分析 （1）根据待定系数法，可得函数解析式，根据自变量与函数值的对应关系，可得C点坐标；
（2）根据面积的和差，可得△ACN，根据△ACN与三角形△ABC的面积的关系，可得关于m的方程，根据解方程，可得m的值，根据自变量与函数值的对应关系，可得答案；
（3）根据勾股定理，可得E点坐标，根据切线与直径垂直，可得切线的方程．

解答 解：（1）将A、B点的坐标代入，得
$\left\{\begin{array}{l}{\frac{4}{3}×9+3b+c=0}\\{\frac{4}{3}×（-1）-b+c=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{b=-\frac{10}{3}}\\{c=-2}\end{array}\right.$，
抛物线的解析式为y=$\frac{4}{3}$x²-$\frac{10}{3}$x-2；
当x=0时，y=-2，即C点坐标（0，-2）；
（2）如图1，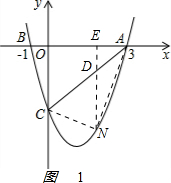
AC的解析式为y=kx+b，将A、C点的坐标代入，得
$\left\{\begin{array}{l}{3k+b=0}\\{b=-2}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=-2}\end{array}\right.$，
AC的解析式为y=$\frac{2}{3}$x-2．
N在抛物线上，D在AC上，设N（m，$\frac{4}{3}$m²-$\frac{10}{3}$m-2），D（m，$\frac{2}{3}$m-2），
DN的长为（$\frac{2}{3}$m-2）-（$\frac{4}{3}$m²-$\frac{10}{3}$m-2）=-$\frac{4}{3}$m²+4m．
S_△ACN=S_△ADN+S_△CDN=$\frac{1}{2}$DN•OE+$\frac{1}{2}$DN•AE=$\frac{1}{2}$DN•AO=$\frac{1}{2}$×3×（-$\frac{4}{3}$m²+4m）．
S_△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×4×2=4．
由△ACN与三角形△ABC的面积比为1：2，得
$\frac{1}{2}$×3×（-$\frac{4}{3}$m²+4m）=2．
m=$\frac{3+\sqrt{5}}{2}$，m=$\frac{3-\sqrt{5}}{2}$，
当m=$\frac{3+\sqrt{5}}{2}$时，y=$\frac{4}{3}$m²-$\frac{10}{3}$m-2=-$\frac{11\sqrt{5}}{3}$-$\frac{7}{3}$，即N（$\frac{3+\sqrt{5}}{2}$，$\frac{-11\sqrt{5}-7}{3}$），
当m=$\frac{3-\sqrt{5}}{2}$时，y=$\frac{4}{3}$m²-$\frac{10}{3}$m-2=$\frac{-35+7\sqrt{5}}{6}$，即N（$\frac{3-\sqrt{5}}{2}$，$\frac{-35+7\sqrt{5}}{6}$），
综上所述：在线段AC下方的抛物线上存在点N，使△ACN与三角形△ABC的面积比为1：2，N的坐标
（$\frac{3+\sqrt{5}}{2}$，$\frac{-11\sqrt{5}-7}{3}$），（$\frac{3-\sqrt{5}}{2}$，$\frac{-35+7\sqrt{5}}{6}$）；
（3）如图2，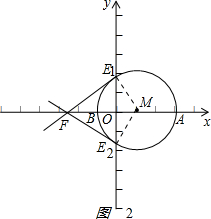
AB的中点M（1，0），ME₁=ME₂=2．
OE₁=OE₂=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，即E₁（0，$\sqrt{3}$），E₂（0，-$\sqrt{3}$）．
设ME₁的解析式为y=kx+b，将M、E₁代入函数解析式解得，ME₁的解析式为y=-$\sqrt{3}$x+$\sqrt{3}$，
由FE₁是⊙M的切线，得
FE₁的解析式为y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$；
设ME₂的解析式为y=kx+b，将M、E₂代入函数解析式解得，
ME₂的解析式为y=$\sqrt{3}$x-$\sqrt{3}$，
由FE₂是⊙M的切线，得
FE₂的解析式为y=-$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$，
综上所述：直线1的函数表达式y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$；y=-$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$．

点评 本题考查了二次函数综合题，利用待定系数法求函数解析式；利用面积的和差得出关于m的方程是解题关键；利用切线垂直于过切点的直径是解题关键．