题目内容
19. A、B两村之间隔一条河,现在要在河上架一座桥.
A、B两村之间隔一条河,现在要在河上架一座桥.(1)要使这两村A、B之间的行程最短,桥应修在何处?请帮他们设计出来.
(2)若两村A、B到河边的距离分别为50米和20米,河宽为30米,AC=40米,你能求出两村的最短路程吗?若能,请求出来.
分析 (1)作AM∥BC,使得AM=30,连接BM与河岸的交点为K,在K处修一条桥KN即可.
(2)在RT△BMH中,利用勾股定理求出BM,最短路程就是BK+KN+AN=BK+KM+KN=MB+KN.
解答 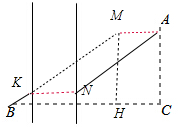 解:(1)桥应该建在如图所示MN处,四边形AMKN是平行四边形.
解:(1)桥应该建在如图所示MN处,四边形AMKN是平行四边形.
(2)作MH⊥BC垂足为H.
两村A、B之间的最短路程=AN+KN+BK,
∵四边形AMKN是平行四边形,
∴AN=MK,
在RT△BMH中,∵BH=70,MH=40,
∴BM=$\sqrt{M{H}^{2}+B{H}^{2}}$=10$\sqrt{65}$,
∴AN+KN+BK=BM+KN=10$\sqrt{65}$+30,
∴两村的最短路程为(10$\sqrt{65}$+30)米.
点评 本题考查的是轴对称-最短路线问题,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
14. 如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.则sin∠E的值为( )
如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.则sin∠E的值为( )
 如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.则sin∠E的值为( )
如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.则sin∠E的值为( )| A. | $\frac{7}{25}$ | B. | $\frac{9}{25}$ | C. | $\frac{14}{25}$ | D. | $\frac{24}{25}$ |
9. 某校为了更好的开展“学校特色体育教育”,从全校七年级各班分别随机抽取了5名男生和5名女生,组成了一个数据个数为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:
某校为了更好的开展“学校特色体育教育”,从全校七年级各班分别随机抽取了5名男生和5名女生,组成了一个数据个数为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:
某校60名学生体育测试成绩频数分布表
(说明:40~55分为不合格,55~70分为合格,70~85分为良好,85~100分为优秀).(注:x~y中的“~”表示大于等于x而小于y)
请根据以上信息,解答下列问题:
(1)表中的a=18,b=50%;
(2)请根据频数分布表,画出相应的频数直方图;
(3)如果该校七年级共有300名学生,根据以上数据,估计该校七年级学生身体素质良好及以上的人数240.
 某校为了更好的开展“学校特色体育教育”,从全校七年级各班分别随机抽取了5名男生和5名女生,组成了一个数据个数为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:
某校为了更好的开展“学校特色体育教育”,从全校七年级各班分别随机抽取了5名男生和5名女生,组成了一个数据个数为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
| 成绩 | 人数(频数) | 百分比 |
| 优秀 | a | 30% |
| 良好 | 30 | b |
| 合格 | 9 | 15% |
| 不合格 | 3 | 5% |
| 合计 | 60 | 100% |
请根据以上信息,解答下列问题:
(1)表中的a=18,b=50%;
(2)请根据频数分布表,画出相应的频数直方图;
(3)如果该校七年级共有300名学生,根据以上数据,估计该校七年级学生身体素质良好及以上的人数240.

 如图,△ABC中,BD为AC边上的中线,BE平分∠CBD交AC于E,F为BC上一点,连接AF分别交BD、BE于H、G,且BH=BF,过C作CK∥AF交BD的延长线于K
如图,△ABC中,BD为AC边上的中线,BE平分∠CBD交AC于E,F为BC上一点,连接AF分别交BD、BE于H、G,且BH=BF,过C作CK∥AF交BD的延长线于K 如图,△ABC中,∠ACB=30°,CD⊥AB于D,E为CD上一点,使得∠CAE=30°,连接BE,求证:∠BED=3∠BCD.
如图,△ABC中,∠ACB=30°,CD⊥AB于D,E为CD上一点,使得∠CAE=30°,连接BE,求证:∠BED=3∠BCD.