题目内容
6.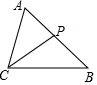 如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )
如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③ |
分析 根据有两组角对应相等的两个三角形相似可对①②进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对③④进行判断.
解答 解:当∠ACP=∠B,∵∠A=∠A,
所以△APC∽△ACB;
当∠APC=∠ACB,∵∠A=∠A,
所以△APC∽△ACB;
当AC2=AP•AB,
即AC:AB=AP:AC,∵∠A=∠A
所以△APC∽△ACB;
当AB•CP=AP•CB,即$\frac{PC}{BC}=\frac{AP}{AB}$,
而∠PAC=∠CAB,
所以不能判断△APC和△ACB相似.
故选D.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
14.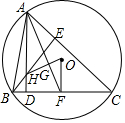 如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )
如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )
 如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )
如图,△ABC的两条高线AD、BE交于H,其外接圆圆心为O,过O作OF垂直BC于F,OH与AF相交于G,则△OFG与△GAH面积之比为( )| A. | 2:4 | B. | 1:3 | C. | 2:5 | D. | 1:4 |
18.当x=$\sqrt{3}$时,代数式$\sqrt{(x-2)^{2}}$+$\root{3}{(1-x)^{3}}$的值是( )
| A. | 3 | B. | 1-2$\sqrt{3}$ | C. | 3-2$\sqrt{3}$ | D. | 2$\sqrt{3}$-1 |

 如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且CF是⊙O的切线.
如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且CF是⊙O的切线.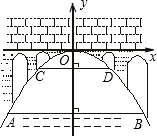 如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m.
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m.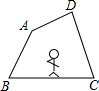 如图,小明沿画在地面上的四边形ABCD的边逆时针走一圈回到原地.
如图,小明沿画在地面上的四边形ABCD的边逆时针走一圈回到原地.