题目内容
8．
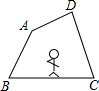如图，小明沿画在地面上的四边形ABCD的边逆时针走一圈回到原地．（1）小明一共旋转的度数是360°；
（2）请在图中标出小明在每个顶点处转过的角度；
（3）小明所转过的角度的总和可以用式子表示为4×180°-（4-2）•180°；
（4）如果顺时针走一圈呢？如果小明沿五边形、六边形、n边形的边走一圈呢？
分析 多边形的外角和指每个顶点处取一个外角，则n边形取n个外角，无论边数是几，其外角和永远为360°，据此判断即可．
解答 解：（1）根据多边形外角和定理可得，小明一共旋转的度数是四边形的外角和，即为360°，
故答案为：360°；
（2）小明在每个顶点处转过的角度如图所示：
（3）小明所转过的角度的总和可以用式子表示为：4×180°-（4-2）•180°；
故答案为：4×180°-360°；
（4）如果顺时针走一圈，小明所转过的角度的总和为360°，如果小明沿五边形、六边形、n边形的边走一圈，小明所转过的角度的总和都为360°．
点评 本题主要考查了多边形的外角和定理：多边形的外角和等于360度． 借助内角和和邻补角概念可以共同推出：外角和=180°n-（n-2）•180°=360°．
练习册系列答案
相关题目
6．
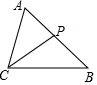如图，△ABC中，P为AB上一点，在下列四个条件中：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AB•CP=AP•CB，能满足△APC和△ACB相似的条件是（ ）
如图，△ABC中，P为AB上一点，在下列四个条件中：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AB•CP=AP•CB，能满足△APC和△ACB相似的条件是（ ）| A． | ①②④ | B． | ①③④ | C． | ②③④ | D． | ①②③ |
4．解方程求出两个根x1、x2，并计算两个根的和与积，完成下表．
（1）补全上述表格；
（2）观察表格中方程两个解的和、两个解的积与原方程的系数之间的关系有什么规律？写出你的结论；（用文字或式子表达）
（3）根据表格中所得的规律解答：已知x1，x2是方程3x2-4x-2=0的两根，求x12+x22的值．
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| 9x2-2=0 | $\frac{\sqrt{2}}{3}$ | -$\frac{\sqrt{2}}{3}$ | 0 | |
| 2x2-3x=0 | 0 | $\frac{3}{2}$ | $\frac{3}{2}$ | 0 |
| x2-3x+2=0 | 1 | 2 | 3 | 2 |
| 关于x的方程ax2+bx+c=0（a≠0，b2-4ac≥0） | $\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$ | $\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$ |
（2）观察表格中方程两个解的和、两个解的积与原方程的系数之间的关系有什么规律？写出你的结论；（用文字或式子表达）
（3）根据表格中所得的规律解答：已知x1，x2是方程3x2-4x-2=0的两根，求x12+x22的值．