题目内容
11.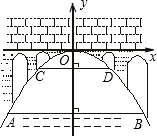 如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m.
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m.(1)在如图所示的直角坐标系下,求此抛物线的解析式;
(2)现有一辆载有救援物资的货车从甲地出发必须经过此桥开往乙地,已知甲地距此桥480km.货车正以每小时40km的速度开往乙地,当行驶1小时时,忽然接到紧急通知:前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位距桥拱最高点3m时,禁止车辆通行),试问:如果货车按原来速度行驶,能否安全通过此桥?若能,请说明理由;若不能,要使货车安全通过此桥,速度应超过每小时多少千米?
(3)当货车接到紧急通知的同时,此桥上游40km处有一船只也接到该通知,此船正以每小时20km的最大速度顺水行驶而来,不知此船能否顺利通过此桥?请说明理由.(已知船的顶部距水面有3.5m高,船体上、下宽均为4m).
分析 (1)根据函数图象可以设出函数解析式,然后根据题目中的数据可以求得此抛物线的解析式;
(2)根据题意可以求得货车按原速到达搭桥的时间,也可以求得安全通过此桥用的时间,然后进行比较即可解答此题;
(3)根据题意可以求得此船到达此桥用的时间,也可以求得升到最大水位用的时间,然后进行比较即可解答此题.
解答 解:(1)设所求抛物线的解析式为:y=ax2,点D的坐标为(5,b),点B(10,b-15),
b=a×52,b-15=a×102,
解得,a=$-\frac{1}{5}$,b=-5,
即抛物线的解析式为y=$-\frac{1}{5}{x}^{2}$;
(2)货车原速行驶到达搭桥所需时间为:480÷40-1=11小时,
∵点D(5,-5),
∴到搭桥禁止通行还有:(5-3)÷0.25=8小时,
∵11>8,
∴货车按原来速度行驶,不能安全通过此桥,
∵(480-40)÷8=55,
∴若要安全通过此桥,则车速应超过55千米/时;
(3)当x=2时,y=$-\frac{1}{5}×{2}^{2}=-0.8$,
∵D(5,-5),
∴5-0.8-3.5=0.7,
即船要顺利通过此桥,水位最多上升0.7米,所需时间为:0.7÷0.25=2.8小时,
∵40÷20=2小时,2.8>2,
∴此船可以安全通过此桥.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,明确图象上点的坐标代表的实际意义.

练习册系列答案
相关题目
1.已知$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组$\left\{\begin{array}{l}{2x+3y+1=0}\\{3x-2y+2=0}\end{array}\right.$的解,则不等式ax-b+1>0的解是( )
| A. | x$<\frac{3}{2}$ | B. | x$<-\frac{3}{2}$ | C. | x$>\frac{3}{2}$ | D. | x$>-\frac{3}{2}$ |
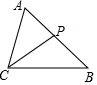 如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )
如图,△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )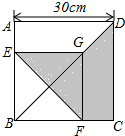 如图,ABCD和EBFG都是正方形,AB=30cm,则阴影部分的面积为450cm2.
如图,ABCD和EBFG都是正方形,AB=30cm,则阴影部分的面积为450cm2.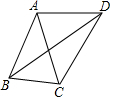 如图,AB=AC=AD,∠CBD=2∠BDC,∠BAC=40°,求∠CAD的度数.
如图,AB=AC=AD,∠CBD=2∠BDC,∠BAC=40°,求∠CAD的度数.