题目内容
11. 如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=( )
如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=( )| A. | $\sqrt{5}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | 7 |
分析 根据直角三角形斜边上的中线等于斜边的一半可得DE=DF=$\frac{1}{2}$AB,EF=$\frac{1}{2}$BC,然后代入数据计算即可得解.
解答 解:∵AF⊥BC,BE⊥AC,D是AB的中点,
∴DE=DF=$\frac{1}{2}$AB,
∵AB=AC,AF⊥BC,
∴点F是BC的中点,∴BF=FC=3,
∵BE⊥AC,
∴EF=$\frac{1}{2}$BC=3,
∴△DEF的周长=DE+DF+EF=AB+3=7,
∴AB=4,
由勾股定理知 AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=$\sqrt{7}$,
故选B.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记各性质是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
3.等腰三角形的底边长10m,周长为36cm,则底角的正弦值为( )
| A. | $\frac{5}{18}$ | B. | $\frac{5}{16}$ | C. | $\frac{13}{15}$ | D. | $\frac{12}{13}$ |
1.一元二次方程x(x-2)=0根的情况是( )
| A. | 只有一个实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
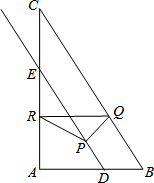 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D在AB上且AD=4,DE∥BC交AC于E,点P从点D出发沿射线DE运动,过点P作PQ⊥BC于Q,过点Q作QR∥AB交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,RQ=y.
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D在AB上且AD=4,DE∥BC交AC于E,点P从点D出发沿射线DE运动,过点P作PQ⊥BC于Q,过点Q作QR∥AB交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,RQ=y.