题目内容
6.解方程组(1)$\left\{\begin{array}{l}{μ+v=10}\\{3μ-2v=5}\end{array}\right.$(用代入法)
(2)$\left\{\begin{array}{l}{2x+3y=14}\\{3x+2y=16}\end{array}\right.$
(3)$\left\{\begin{array}{l}{2p-3q=13}\\{-p+5=4q}\end{array}\right.$
(4)$\left\{\begin{array}{l}{\frac{m}{2}+\frac{n}{3}=13}\\{\frac{m}{3}-\frac{n}{4}=3}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可;
(3)方程组利用加减消元法求出解即可;
(4)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{μ+v=10①}\\{3μ-2v=5②}\end{array}\right.$,
由①得:μ=10-v③,
③代入②得:30-3v-2v=5,即v=5,
把v=5代入③得:μ=5,
则方程组的解为$\left\{\begin{array}{l}{μ=5}\\{v=5}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+3y=14①}\\{3x+2y=16②}\end{array}\right.$,
①+②得:5(x+y)=30,即x+y=6③,
①-③×2得:y=2,
把y=2代入③得:x=4,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{2p-3q=13①}\\{p+4q=5②}\end{array}\right.$,
①×4+②×3得:11p=67,即p=$\frac{67}{11}$,
把p=$\frac{67}{11}$代入②得:q=-$\frac{3}{11}$,
则方程组的解为$\left\{\begin{array}{l}{p=\frac{67}{11}}\\{q=-\frac{3}{11}}\end{array}\right.$;
(4)方程组整理得:$\left\{\begin{array}{l}{3m+2n=78①}\\{4m-3n=36②}\end{array}\right.$,
①×3+②×2得:m=18,
把m=18代入①得:n=12,
则方程组的解为$\left\{\begin{array}{l}{m=18}\\{n=12}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

| A. | 50° | B. | 80° | C. | 65° | D. | 50°或80° |
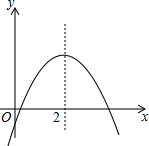 二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )①ab<0,②ac<0,③当x<2时,函数值随x增大而增大;当x>2时,函数值随x增大而减小,④二次函数y=ax2+bx+c的图象与x轴交点的横坐标就是方程ax2+bx+c=0的根.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=( )
如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=( )| A. | $\sqrt{5}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | 7 |
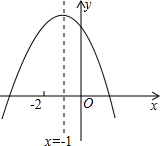 已知二次函数y=ax2+bx=c的图象如图,下列结论:
已知二次函数y=ax2+bx=c的图象如图,下列结论: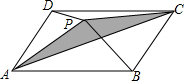 如图,P是?ABCD内一点,且S△PAB=8,S△PAD=5,则阴影部分的面积为3.
如图,P是?ABCD内一点,且S△PAB=8,S△PAD=5,则阴影部分的面积为3.