题目内容
2.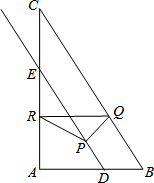 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D在AB上且AD=4,DE∥BC交AC于E,点P从点D出发沿射线DE运动,过点P作PQ⊥BC于Q,过点Q作QR∥AB交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,RQ=y.
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D在AB上且AD=4,DE∥BC交AC于E,点P从点D出发沿射线DE运动,过点P作PQ⊥BC于Q,过点Q作QR∥AB交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,RQ=y.(1)求y关于x的函数关系式;
(2)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由;
(3)当x怎样时,以Q为圆心,RP长为半径的圆与射线DE只有一个交点.
分析 (1)首先在Rt△ABC中,根据勾股定理,求出BC边的长度是多少;然后根据QR∥AB,可得$\frac{RQ}{AB}=\frac{CQ}{CB}$,据此求出y关于x的函数关系式即可.
(2)根据题意,分三种情况:①当PQ=PR时;②当PR=QR时;③当PQ=RQ时;然后根据等腰三角形的性质,分类讨论,求出所有满足要求的x的值即可.
(3)根据题意,分三种情况:①当PQ=PR时;②当点Q与点C重合时;③以Q为圆心,RP长为半径的圆与DE所在的直线有2个交点,但是它与射线DE只有一个交点时,分类讨论,求出所有满足要求的x的值即可.
解答 解:(1)在Rt△ABC中,
BC=$\sqrt{{AB}^{2}{+AC}^{2}}=\sqrt{{6}^{2}{+8}^{2}}=10$,
∵QR∥AB,
∴$\frac{RQ}{AB}=\frac{CQ}{CB}$,
即$\frac{y}{6}=\frac{10-x}{10}$,
∴$y=6-\frac{3}{5}x$.
(2)①如图1,当PQ=PR时,作PF⊥RQ于F,作DG⊥BC于G,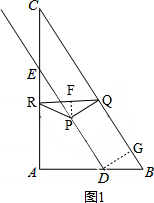 ,
,
在△BGD和△BAC中,
$\left\{\begin{array}{l}{∠B=∠B}\\{∠BGD=∠BAC}\end{array}\right.$,
∴△BGD∽△BAC,
∴$\frac{GD}{AC}=\frac{BD}{BC}=\frac{6-4}{10}=\frac{1}{5}$,
∴GD=$\frac{1}{5}×8=\frac{8}{5}$,
∵PQ=PR,PF⊥RQ,
∴RF=FQ,
∵∠C+∠CQR=∠FQP+∠CQR,
∴∠FQP=∠C,
∴cos∠FQP=cos∠C=$\frac{AC}{BC}=\frac{8}{10}$=$\frac{4}{5}$,
∴$\frac{FQ}{PQ}=\frac{FQ}{GD}=\frac{4}{5}$,
∴$\frac{\frac{1}{2}×(6-\frac{3}{5}x)}{\frac{8}{5}}=\frac{4}{5}$,
解得x=$\frac{86}{15}$.
②如图2,当PR=QR时,作EM⊥BC于M,作RN⊥EM于N,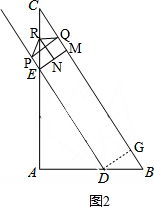 ,
,
∵PQ⊥BC,EM⊥BC,
∴PQ∥EM,
∵PR=QR,RN⊥EM,
∴EN=MN,
∵RN∥BC,
∴$\frac{ER}{CR}=\frac{EN}{MN}=1$,
∴ER=CR,
∵DE∥BC,
∴$\frac{AE}{CE}=\frac{AD}{DB}=\frac{4}{2}=2$,
∴AE=2CE,AE+CE=8,
∴CE=$\frac{8}{3}$,CR=$\frac{1}{2}×\frac{8}{3}=\frac{4}{3}$,
∴tan∠C=$\frac{RQ}{CR}=\frac{6-\frac{3}{5}x}{\frac{4}{3}}=\frac{6}{8}=\frac{3}{4}$,
解得x=$\frac{25}{3}$.
③当PQ=RQ时,
6-$\frac{3}{5}x=\frac{8}{5}$,
解得x=$\frac{22}{3}$.
综上,可得
$x=\frac{86}{15}$,x=$\frac{25}{3}$或x=$\frac{22}{3}$时,△PQR为等腰三角形.
(3)①当PQ=PR时,
以Q为圆心,RP长为半径的圆与射线DE相切,只有一个交点,
由(2),可得x=$\frac{86}{15}$,
∴当x=$\frac{86}{15}$时,以Q为圆心,RP长为半径的圆与射线DE只有一个交点.
②如图3,当点Q与点C重合时,点R也与点C重合,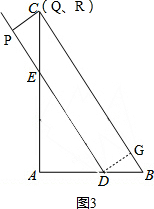 ,
,
以Q为圆心,RP长为半径的圆与射线DE相切,只有一个交点,
此时x=BC=10,
∴当x=10时,以Q为圆心,RP长为半径的圆与射线DE只有一个交点.
③如图4,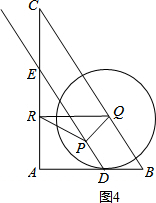 ,
,
以Q为圆心,RP长为半径的圆与DE所在的直线有2个交点,但是它与射线DE只有一个交点时,
10x2+51x-300=0,
∴当$\frac{6}{5}$≤x≤$\frac{{-51+\sqrt{14601}}}{20}$时,以Q为圆心,RP长为半径的圆与射线DE只有一个交点.
综上,可得$x=\frac{86}{15}$,x=10或$\frac{6}{5}$≤x≤$\frac{{-51+\sqrt{14601}}}{20}$时,以Q为圆心,RP长为半径的圆与射线DE只有一个交点.
点评 (1)此题主要考查了圆的综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合的方法,要熟练掌握,
(2)此题还考查了直角三角形、等腰三角形的性质和应用,以及勾股定理的应用,要熟练掌握.
(3)此题还考查了相似三角形的性质和应用,要熟练掌握.

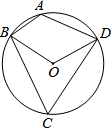 如图,A,B,C,D为⊙O上四点,若∠BOD=110°,则∠A的度数是( )
如图,A,B,C,D为⊙O上四点,若∠BOD=110°,则∠A的度数是( )| A. | 110° | B. | 115° | C. | 120° | D. | 125° |
| A. | x2•x3=x6 | B. | (x2)3=x5 | C. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | D. | x5-x2=x3 |
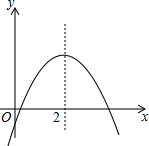 二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )①ab<0,②ac<0,③当x<2时,函数值随x增大而增大;当x>2时,函数值随x增大而减小,④二次函数y=ax2+bx+c的图象与x轴交点的横坐标就是方程ax2+bx+c=0的根.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=( )
如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=( )| A. | $\sqrt{5}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | 7 |
| A. | a5 | B. | a6 | C. | -a5 | D. | -a6 |
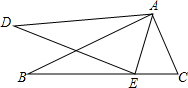 如图,在△ABC和△ADE中,点E在BC上,∠B=∠D,AB=AD,∠EAC=∠DAB
如图,在△ABC和△ADE中,点E在BC上,∠B=∠D,AB=AD,∠EAC=∠DAB