题目内容
3.等腰三角形的底边长10m,周长为36cm,则底角的正弦值为( )| A. | $\frac{5}{18}$ | B. | $\frac{5}{16}$ | C. | $\frac{13}{15}$ | D. | $\frac{12}{13}$ |
分析 先画出几何图形,AB=AC,BC=10cm,AB+BC+AC=36cm,则AB=AC=13cm,作AD⊥BC于D,根据等腰三角形的性质得BD=$\frac{1}{2}$BC=5,则利用勾股定理可计算出AD=12,然后根据正弦的定义求解.
解答 解: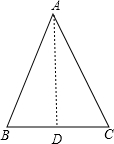 如图,AB=AC,BC=10cm,AB+BC+AC=36cm,则AB=AC=13cm,
如图,AB=AC,BC=10cm,AB+BC+AC=36cm,则AB=AC=13cm,
作AD⊥BC于D,
∵AB=AC,
∴BD=CD=$\frac{1}{2}$BC=5,
在Rt△ABD中,∵AB=13,BD=5,
∴AD=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴tanB=$\frac{AD}{AB}$=$\frac{12}{13}$.
故选D.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了等腰三角形的性质.

练习册系列答案
相关题目
19.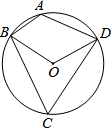 如图,A,B,C,D为⊙O上四点,若∠BOD=110°,则∠A的度数是( )
如图,A,B,C,D为⊙O上四点,若∠BOD=110°,则∠A的度数是( )
 如图,A,B,C,D为⊙O上四点,若∠BOD=110°,则∠A的度数是( )
如图,A,B,C,D为⊙O上四点,若∠BOD=110°,则∠A的度数是( )| A. | 110° | B. | 115° | C. | 120° | D. | 125° |
14.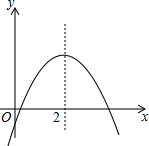 二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )
①ab<0,②ac<0,③当x<2时,函数值随x增大而增大;当x>2时,函数值随x增大而减小,④二次函数y=ax2+bx+c的图象与x轴交点的横坐标就是方程ax2+bx+c=0的根.
 二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论正确的有( )①ab<0,②ac<0,③当x<2时,函数值随x增大而增大;当x>2时,函数值随x增大而减小,④二次函数y=ax2+bx+c的图象与x轴交点的横坐标就是方程ax2+bx+c=0的根.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11. 如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=( )
如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=( )
 如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=( )
如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=( )| A. | $\sqrt{5}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | 7 |
8.为了解某市数学中考成绩,从中随机抽取了3000名考生进行调查,这项调查中的样本是( )
| A. | 某市数学中考成绩 | |
| B. | 从中抽取的3000名考生 | |
| C. | 从中抽取的3000名考生的数学中考成绩 | |
| D. | 3000 |
12.(-a2)3=( )
| A. | a5 | B. | a6 | C. | -a5 | D. | -a6 |
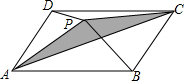 如图,P是?ABCD内一点,且S△PAB=8,S△PAD=5,则阴影部分的面积为3.
如图,P是?ABCD内一点,且S△PAB=8,S△PAD=5,则阴影部分的面积为3.