题目内容
7．计算：$\root{3}{8}-|{-2}|+{（{\frac{1}{3}}）^{-2}}$-4cos60°．分析 原式第一项利用立方根定义计算，第二项利用绝对值的代数意义化简，第三项利用负整数指数幂法则计算，最后一项利用特殊角的三角函数值计算即可得到结果．
解答 解：原式=2-2+9-4×$\frac{1}{2}$=7．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
17．
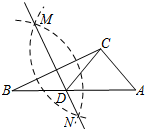如图，在已知的△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于$\frac{1}{2}$BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠A=50°，则∠ACB的度数为（ ）
如图，在已知的△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于$\frac{1}{2}$BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠A=50°，则∠ACB的度数为（ ）
| A． | 90° | B． | 95° | C． | 100° | D． | 105° |
2．等腰三角形一个角的度数为50°，则顶角的度数为（ ）
| A． | 50° | B． | 80° | C． | 65° | D． | 50°或80° |
12．-$\frac{2}{5}$的倒数是（ ）
| A． | -$\frac{5}{2}$ | B． | $\frac{5}{2}$ | C． | -$\frac{2}{5}$ | D． | $\frac{2}{5}$ |
19．
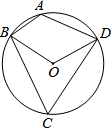如图，A，B，C，D为⊙O上四点，若∠BOD=110°，则∠A的度数是（ ）
如图，A，B，C，D为⊙O上四点，若∠BOD=110°，则∠A的度数是（ ）| A． | 110° | B． | 115° | C． | 120° | D． | 125° |
16．下列计算正确的是（ ）
| A． | x2•x3=x6 | B． | （x2）3=x5 | C． | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | D． | x5-x2=x3 |
11．
如图，在三角形ABC中，AB=AC，BC=6，三角形DEF的周长是7，AF⊥BC于F，BE⊥AC于E，且点D是AB的中点，则AF=（ ）
如图，在三角形ABC中，AB=AC，BC=6，三角形DEF的周长是7，AF⊥BC于F，BE⊥AC于E，且点D是AB的中点，则AF=（ ）| A． | $\sqrt{5}$ | B． | $\sqrt{7}$ | C． | $\sqrt{3}$ | D． | 7 |