题目内容
18.河上有一座抛物线拱桥,已知桥下的水面离桥孔顶部3米时,水面宽6米,当水位上升1米时,水面宽为多少米(精确到0.1米)?分析 据题意假设函数解析式为y=ax2+c,然后根据题中数据代入求值.
解答 解:设函数解析式为y=ax2+c,
由题意得,x=3时,y=0,x=0时,y=3,
∴$\left\{\begin{array}{l}{0=9a+c}\\{c=3}\end{array}\right.$,
解得a=-$\frac{1}{3}$,c=3,
即y=-$\frac{1}{3}$x2+3,
当水位上升1米时,y=1,
即1=-$\frac{1}{3}$x2+3,
解得x=±$\sqrt{6}$,
2$\sqrt{6}$≈4.9,
此时水面宽度为4.9米.
点评 此题主要考查了二次函数的应用以及图象上点的坐标性质,根据题意确定点的坐标是解题关键.

练习册系列答案
相关题目
8.△ABC中,点D在边BC上,已知AB=AD=2,AC=4,且BD:DC=2:3,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
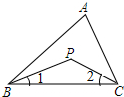 如图,P是△ABC内一点,连结PB、PC.
如图,P是△ABC内一点,连结PB、PC.