题目内容
13.在定圆内有两条互相垂直的弦AC、BD,求证:AB2+BC2+CD2+DA2为定值.分析 作OE⊥AC于E,OF⊥BD于F,连接OA,OB,OC,OD,设⊙O的半径为R(定值),AC,BD的交点为H,AC=2a,BD=2b,利用垂径定理可得AE=CE=a,BF=CF=b,OE=FH,OF=EH,由勾股定理得a2+b2+EH2+FH2=2R2,等量代换得出结论.
解答  证明:作OE⊥AC于E,OF⊥BD于F,连接OA,OB,OC,OD,
证明:作OE⊥AC于E,OF⊥BD于F,连接OA,OB,OC,OD,
设⊙O的半径为R(定值),AC,BD的交点为H,AC=2a,BD=2b,
则AE=CE=a,BF=CF=b,OE=FH,OF=EH,OE2+a2=R2,OF2+b2=R2,
∴a2+b2+EH2+FH2=2R2,
∵AC⊥BD,
∴AB2+BC2+CD2+DA2=2AH2+2BH2+2CH2+2DH2
=2(a+EH)2+2(b-HF)2+2(a-EH)2+2(b+FH)2
=4(a2+b2+EH2+FH2)
=8R2
=定值.
点评 本题主要考查了垂径定理和勾股定理,作出适当的辅助线,设半径为定值R是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
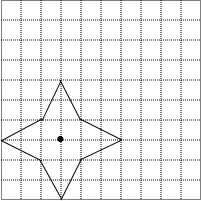 如图,一朵四瓣花飘动在10×10的网格中.
如图,一朵四瓣花飘动在10×10的网格中.
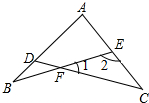 如图,∠B=25°,∠C=35°,∠A-∠1=60°,求∠A的度数.
如图,∠B=25°,∠C=35°,∠A-∠1=60°,求∠A的度数.