题目内容
10.计算题:(1)$\frac{y}{4{x}^{2}y}-\frac{1}{12{y}^{2}}+\frac{1}{6xy}$
(2)$\frac{{a}^{2}}{a-1}-a-1$.
分析 (1)原式通分并利用同分母分式的加减法则计算即可得到结果;
(2)原式通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=$\frac{3{y}^{2}-{x}^{2}+2xy}{12{x}^{2}{y}^{2}}$;
(2)原式=$\frac{{a}^{2}-(a+1)(a-1)}{a-1}$=$\frac{1}{a-1}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.定义函数y=[x•[x]],其中[x]表示不超过x的最大整数,如:[1.5]=1,[-1.3]=-2.当x∈[0,n)(n∈N*)时,记an为函数y的所有可能取值的个数.则a10=( )
| A. | 45 | B. | 46 | C. | 55 | D. | 66 |
15.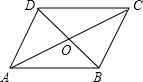 如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )
如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )
 如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )
如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )| A. | 1<m<11 | B. | 2<m<22 | C. | 10<m<12 | D. | 5<m<6 |
 已知AB∥CD,直线MN分别交AB,CD于E、F,∠MFD=50°,EG平分∠MEB,求∠MEG的度数.
已知AB∥CD,直线MN分别交AB,CD于E、F,∠MFD=50°,EG平分∠MEB,求∠MEG的度数.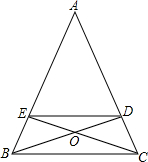 已知,如图,△ABC中,AB=AC,BD,CE为△ABC的高,且BD,CE交于点O.
已知,如图,△ABC中,AB=AC,BD,CE为△ABC的高,且BD,CE交于点O.