题目内容
8．△ABC中，点D在边BC上，已知AB=AD=2，AC=4，且BD：DC=2：3，则△ABC是（ ）| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 无法确定 |
分析 过A作AE⊥BD，设BD=2x，CD=3x，根据等腰三角形的性质可得BE=ED=x，再根据勾股定理可得42-（x+3x）2=22-x2，解方程可得x的值，进而可得BC长，再利用勾股定理逆定理可得△ABC是直角三角形．
解答 
解：过A作AE⊥BD，
∵BD：DC=2：3，
∴设BD=2x，CD=3x，
∵AB=AD，AE⊥BD，
∴BE=ED=x，
由勾股定理可得：42-（x+3x）2=22-x2，
解得：$x=\frac{{2\sqrt{5}}}{5}$，
∴$BC=2\sqrt{5}$，
∵22+42=（2$\sqrt{5}$）2，
∴△ABC是直角三角形，
故选：B．
点评 此题主要考查了勾股定理逆定理，关键是正确画出图形，作出辅助线，利用勾股定理计算出BC长．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
18．若n为正整数，则$\root{2n+1}{-1}$等于（ ）
| A． | -1 | B． | 1 | C． | ±1 | D． | 2n+1 |
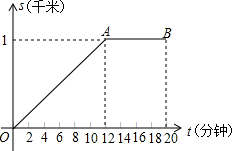小亮早晨从家里出发匀速步行去上学，小亮的妈妈在小亮出发后10分钟，发现小亮的数学课本没带，于是她带上课本立即匀速骑车按小亮上学的路线追赶小亮，结果与小亮同时到达学校．已知小亮在整个上学途中，他出发后t分钟时，他所在的位置与家的距离为s千米，且s与t之间的函数关系的图象如图中的折线段OA-AB所示．
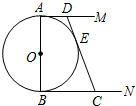如图，⊙O的直径AB=2，AM和BN是它的两条切线，DE切⊙O于E，交AM于D，交BN 于C．设AD=x，BC=y． 
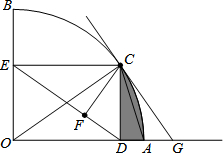如图，扇形OAB的半径OA=3，圆心角∠AOB=90°，点C是弧AB上异于A、B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，连结DE，点F在线段DE上，且EF=2DF，过点C的直线CG交OA的延长线于点G，且∠CGO=∠CDE．