题目内容
2.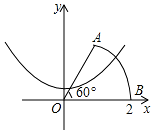 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )| A. | -4<k<$\frac{3}{4}$ | B. | -2<k<$\frac{3}{4}$ | C. | -4<k<$\sqrt{3}$-1 | D. | -2<k<$\sqrt{3}$+1 |
分析 作AC⊥OB于C,利用正弦、余弦的概念求出点A的坐标,根据待定系数法求出直线OA的解析式,联立抛物线解析式得到抛物线与OA相切时k的值,把点B的坐标代入抛物线的解析式求出k,根据题意解答即可.
解答 解:作AC⊥OB于C,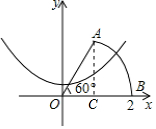
在Rt△AOC中,OC=$\frac{1}{2}$OA=1,AC=OA×sin60°=$\sqrt{3}$,
∴点A的坐标为(1,$\sqrt{3}$),
设直线OA的解析式为y=mx,则m=$\sqrt{3}$,
则直线OA的解析式为y=$\sqrt{3}$x,
联立抛物线解析式得x2+k=$\sqrt{3}$x,即x2-$\sqrt{3}$x+k=0,
△=3-4k=0,
解得k=$\frac{3}{4}$
当抛物线经过当B时,0=4+k,
解得k=-4,
∴抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是-4<k<$\frac{3}{4}$.
故选:C.
点评 本题考查的是二次函数图象与系数的关系以及软件三角函数的概念的应用,根据题意求出点A的坐标、灵活运用分情况讨论思想是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.为了分析学生数学竞赛成绩,指导老师对全体参赛选手的竞赛成绩进行统计,结果如下(单位;分);
91 68 73 90 87 71 61 75 82 77 80 82 93 85 76
78 87 74 88 65 72 86 71 69 72 79 81 90 66 70
75 82 77 78 75 85 72 95 80 79 77 78 83 80 83
(1)填写下面的频数分布表.
当分数在60~74时,成绩为及格;当分数在75~84时,成绩为良好;当分数在85~100时,成绩为优秀,请用扇形图表示出及格、良好、优秀所占的百分比.
91 68 73 90 87 71 61 75 82 77 80 82 93 85 76
78 87 74 88 65 72 86 71 69 72 79 81 90 66 70
75 82 77 78 75 85 72 95 80 79 77 78 83 80 83
(1)填写下面的频数分布表.
| 分组 | 划记 | 频数 |
| 60.5~65.5 |  | 2 |
| 65.5~70.5 |  | 4 |
| 70.5~75.5 |   | 10 |
| 75.5~80.5 |  | 12 |
| 80.5~85.5 |  | 8 |
| 85.5~90.5 |  | 6 |
| 90.5~95.5 |  | 3 |
| 合计 |
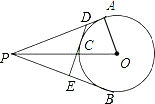 如图,PA、PB、DE分别切圆O于点A、B、C,如果PO=10cm,△PDE的周长为12cm,那么圆O的半径为8cm.
如图,PA、PB、DE分别切圆O于点A、B、C,如果PO=10cm,△PDE的周长为12cm,那么圆O的半径为8cm.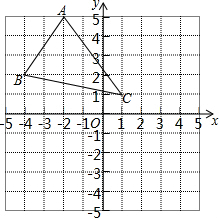 如图所示,三角形ABC的三个顶点的坐标分别是A(-2,5),B(-4,2),C(1,1),将三角形ABC向右平移3个单位长度后,再向下平移5个单位长度,可以得到三角形A′B′C′.
如图所示,三角形ABC的三个顶点的坐标分别是A(-2,5),B(-4,2),C(1,1),将三角形ABC向右平移3个单位长度后,再向下平移5个单位长度,可以得到三角形A′B′C′. 请你给如图建立平面直角坐标系,使文化宫的坐标为(-3,1),超市的坐标为(2,-3).
请你给如图建立平面直角坐标系,使文化宫的坐标为(-3,1),超市的坐标为(2,-3).