题目内容
13.(1)(π-5)0+$\sqrt{2}$cos45°-|-3|+($\frac{1}{2}$)-1(2)先化简,再求值:(1-$\frac{1}{x+2}$)÷$\frac{{x}^{2}+2x+1}{x+2}$,其中$x=\sqrt{3}-1$.
分析 (1)根据零指数幂的意义、负整数指数幂的意义,特殊角的锐角三角函数值即可求出答案.
(2)根据分式的运算法则即可求出答案.
解答 解:(1)原式=1+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-3+2
=1+1-3+2
=1
(2)原式=$\frac{x+1}{x+2}÷\frac{{{{({x+1})}^2}}}{x+2}$
=$\frac{x+1}{x+2}×\frac{x+2}{{{{({x+1})}^2}}}=\frac{1}{x+1}$.
当$x=\sqrt{3}-1$时,
原式=$\frac{1}{{\sqrt{3}-1+1}}=\frac{1}{{\sqrt{3}}}=\frac{{\sqrt{3}}}{3}$.
点评 本题考查学生的运算能力,解题的关键熟练运用运算法则,本题属于基础题型.

练习册系列答案
相关题目
18.东岳中学初四年级进行了一次模拟考试,参加人数为1016人,为了了解这次考试的成绩情况,下列抽取样本合理的是( )
| A. | 抽取前100名学生的成绩 | B. | 抽取后100名学生的成绩 | ||
| C. | 抽取(1)(2)两个班的学生成绩 | D. | 抽取学号为4的倍数的学生的成绩 |
2.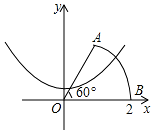 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )
 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )| A. | -4<k<$\frac{3}{4}$ | B. | -2<k<$\frac{3}{4}$ | C. | -4<k<$\sqrt{3}$-1 | D. | -2<k<$\sqrt{3}$+1 |
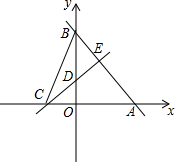 如图,直线y=-$\frac{4}{3}$x+8分别交x轴、y轴于A,B两点.线段AB的垂直平分线分别交x轴、y轴于C,D两点.
如图,直线y=-$\frac{4}{3}$x+8分别交x轴、y轴于A,B两点.线段AB的垂直平分线分别交x轴、y轴于C,D两点.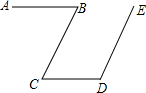 如图,已知AB∥CD,BC∥ED,请你猜想∠B与∠D之间具有什么数量关系,并说明理由.
如图,已知AB∥CD,BC∥ED,请你猜想∠B与∠D之间具有什么数量关系,并说明理由.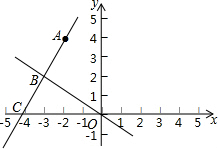 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-$\frac{2}{3}$x的图象交于点B(m,2)
如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-$\frac{2}{3}$x的图象交于点B(m,2) (1)如图,MN∥EF,GH∥EF,∠CAB=90°,∠1=70°,求:∠ABF的度数.
(1)如图,MN∥EF,GH∥EF,∠CAB=90°,∠1=70°,求:∠ABF的度数.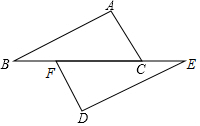 如图,已知点B、F、C、E在同一条直线上,AB∥DE,且AB=DE,∠A=∠D.
如图,已知点B、F、C、E在同一条直线上,AB∥DE,且AB=DE,∠A=∠D.