题目内容
12.(1)计算:$\sqrt{1-\frac{9}{25}}$+$\sqrt{0.04}$+$\root{3}{(-2)^{3}}$+|$\sqrt{\frac{1}{4}}$-1|;(2)已知$\sqrt{{a}^{3}+27}$+|b3-64|=0,求b-a的平方根.
分析 (1)根据算术平方根、立方根、绝对值可以解答本题;
(2)根据非负数的性质可以求得a、b的值,从而可以解答本题.
解答 解:(1)$\sqrt{1-\frac{9}{25}}$+$\sqrt{0.04}$+$\root{3}{(-2)^{3}}$+|$\sqrt{\frac{1}{4}}$-1|
=$\sqrt{\frac{16}{25}}+0.2+(-2)+|\frac{1}{2}-1|$
=$\frac{4}{5}+\frac{1}{5}-2+\frac{1}{2}$
=-$\frac{1}{2}$;
(2)∵$\sqrt{{a}^{3}+27}$+|b3-64|=0,
∴$\left\{\begin{array}{l}{{a}^{3}+27=0}\\{{b}^{3}-64=0}\end{array}\right.$,得$\left\{\begin{array}{l}{a=-3}\\{b=4}\end{array}\right.$,
∴$±\sqrt{b-a}=±\sqrt{4-(-3)}=±\sqrt{7}$,
即b-a的平方根是$±\sqrt{7}$.
点评 本题考查实数的运算、非负数的性质、平方根,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
2.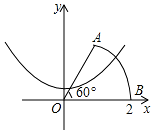 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )
 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )| A. | -4<k<$\frac{3}{4}$ | B. | -2<k<$\frac{3}{4}$ | C. | -4<k<$\sqrt{3}$-1 | D. | -2<k<$\sqrt{3}$+1 |
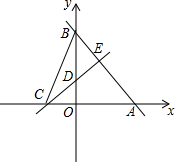 如图,直线y=-$\frac{4}{3}$x+8分别交x轴、y轴于A,B两点.线段AB的垂直平分线分别交x轴、y轴于C,D两点.
如图,直线y=-$\frac{4}{3}$x+8分别交x轴、y轴于A,B两点.线段AB的垂直平分线分别交x轴、y轴于C,D两点.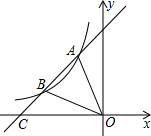 如图,直线y=mx+b与反比例函数y=$\frac{k}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
如图,直线y=mx+b与反比例函数y=$\frac{k}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.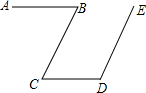 如图,已知AB∥CD,BC∥ED,请你猜想∠B与∠D之间具有什么数量关系,并说明理由.
如图,已知AB∥CD,BC∥ED,请你猜想∠B与∠D之间具有什么数量关系,并说明理由.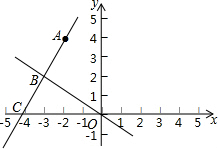 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-$\frac{2}{3}$x的图象交于点B(m,2)
如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-$\frac{2}{3}$x的图象交于点B(m,2)