题目内容
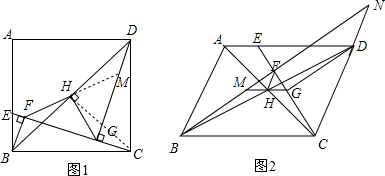
2.如图,在四边形ABCD中,线段CE交四边形的边于点E,点H为BD中点,BF,DG分别垂直CE于点F和点G,连接HF,HG.(1)如图1,若四边形ABCD为正方形,AB=3,AE=2EB,求BF的长;
(2)如图1,若四边形ABCD为正方形,试猜想FG与HF的数量关系,并说明理由;
(3)如图2,若四边形ABCD为平行四边形,CE平分∠BCD且交AD于点E,其他条件不变,求证:AE=HF+HG.
分析 (1)利用面积法来求BF的长度;
(2)通过全等三角形的判定与性质得到△BFC≌△CGD、△HBF≌△HCG,则推知△FGH为等腰直角三角形,所以FG=$\sqrt{2}$HF;
(3)延长GH交BF于点M.由全等三角形的判定定理推知△BHM≌△DHG,则由该全等三角形的性质、直角三角形斜边上中线的性质证得FH=GH=MH,易证:AH=HC,EG=GC,所以AE=2HG,故AE=HF+HG.
解答 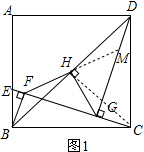 解:(1)如图1,∵四边形ABCD为正方形,AB=3,AE=2EB,
解:(1)如图1,∵四边形ABCD为正方形,AB=3,AE=2EB,
∴BC=AB=3,AE=2,BE=1,
∴在直角△BEC中,由勾股定理得到:CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
则$\frac{1}{2}$BE•BC=$\frac{1}{2}$CE•BF,
故BF=$\frac{BE•BC}{CE}$=$\frac{1×3}{\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$;
(2)如图1,FG=$\sqrt{2}$HF.理由如下:
∵在△BFC与△CGD中,$\left\{\begin{array}{l}{∠BCF=∠CDG}\\{∠BFC=∠CGD}\\{BC=CD}\end{array}\right.$,
∴△BFC≌△CGD(AAS),
∴BF=CG,∠FBC=∠DCG.
∵点H是BD的中点,
∴CH⊥BD,且HC=BH=DH,
∴∠HBC=∠HCD=45°,
∴∠FBH=∠GHC.
∵在△HBF与△HCG中,$\left\{\begin{array}{l}{BF=CG}\\{∠FBH=∠GCH}\\{BH=CH}\end{array}\right.$,
∴△HBF≌△HCG(SAS),
∴FH=GH,∠FHB=∠GHC,
∴∠FHG=∠BHC=90°,
∴FG=$\sqrt{2}$HF;
(3)证明:如图2,∵BF,DG分别垂直CE于点F和点G,
∴BF∥DG.
又∵BH=HD,
∴∠MHB=∠GDH.
∵在△BHM与△DHG中,$\left\{\begin{array}{l}{∠MBH=∠GDH}\\{BH=DH}\\{∠MHB=∠GHD}\end{array}\right.$,
∴△BHM≌△DHG(ASA),
∴HM=HG.
∵∠MFG=90°,
∴FH=GH=MH,
易证AH=HC,EG=GC,
∴AE=2HG,
故AE=HF+HG.
点评 本题综合考查了等腰三角形的判定与性质、正方形(平行四边形的性质以及全等三角形的判定与性质,熟记以上图形的性质并能灵活运用其性质是解答本题的关键,综合性较强,难度较大.

 阅读快车系列答案
阅读快车系列答案| A. | (2a2)4=8a6 | B. | a3+a=a4 | C. | (a-b)2=a2-b2 | D. | a2÷a=a |
| A. | 57° | B. | 66° | C. | 48° | D. | 78° |
 已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.
已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.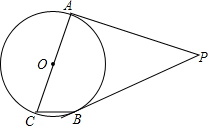 如图:PA、PB是⊙O的切线,切点为A、B,AC是直径,若∠P=50°,则∠ACB=65°.
如图:PA、PB是⊙O的切线,切点为A、B,AC是直径,若∠P=50°,则∠ACB=65°.