题目内容
10. 已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.
已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.(1)当点F与点B重合时,求CP的长;
(2)当点F在CB边上时,设CP=x,PE=y,求y关于x的函数解析式,并写出函数定义域;
(3)当EF=CP时,求CP的长.
分析 (1)证明∠BPC=90°,根据直角三角形的性质求出CP的长;
(2)作FH⊥EP于H,根据直角三角形的性质求出FC、PF的长,根据余弦的概念求出PH的长,根据矩形的性质求出EH,得到y关于x的函数解析式;
(3)作PG⊥BC于G,证明Rt△EBF≌Rt△PGC,得到∠EFB=∠C,得到四边形EFCP是平行四边形,根据平行四边形的性质计算即可.
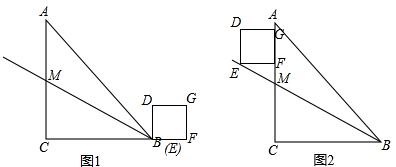
解答 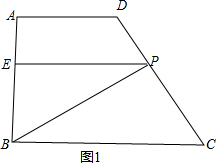 解:(1)当点F与点B重合时,如图1,
解:(1)当点F与点B重合时,如图1,
∵EP∥BC,
∴∠PBC=∠EPB=30°,又∠C=60°,
∴∠BPC=90°,
∴CP=$\frac{1}{2}$BC=$\frac{9}{2}$;
(2)如图2,作FH⊥EP于H,
∵∠BPC=90°,∠C=60°,CP=x,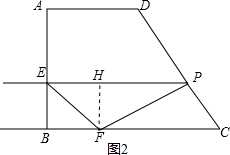 ∴FC=2x,
∴FC=2x,
∴FP=$\sqrt{3}$x,又∠EPF=30°,
∴cos30°=$\frac{PH}{PF}$,
∴PH=$\frac{3}{2}$x,
∵四边形EBFH是矩形,
∴EH=BF=9-2x,
∴y=$\frac{3}{2}$x+9-2x=9-$\frac{1}{2}$x(0≤x≤$\frac{9}{2}$);
(3)当EF=CP时,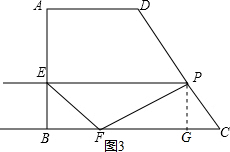 如图3,
如图3,
作PG⊥BC于G,
在Rt△EBF和Rt△PGC中,
$\left\{\begin{array}{l}{EB=PG}\\{EF=PC}\end{array}\right.$,
∴Rt△EBF≌Rt△PGC,
∴∠EFB=∠C=30°,
∴EF∥PC,又EP∥BC,
∴四边形EFCP是平行四边形,
∴EP=FC,
即9-$\frac{1}{2}$x=2x,
解得x=$\frac{18}{5}$.
点评 本题考查的是直角梯形的性质、平行四边形的性质和判定,正确作出辅助线、灵活运用锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
 △ABC中,∠ABC=120°,以AC为边向形外作等边三角形ACD,求证:BD=AB+BC.
△ABC中,∠ABC=120°,以AC为边向形外作等边三角形ACD,求证:BD=AB+BC.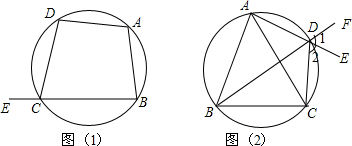
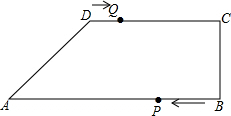 四边形ABCD中,AB∥CD,CB⊥CD,AB=18cm,BC=6cm,CD=10cm,点P在线段BA上从B向A运动,速度为2cm/s,点Q在线段DC上从D向C运动,速度为1cm/s,P,Q两点同时开始运动.设运动时间为T秒.
四边形ABCD中,AB∥CD,CB⊥CD,AB=18cm,BC=6cm,CD=10cm,点P在线段BA上从B向A运动,速度为2cm/s,点Q在线段DC上从D向C运动,速度为1cm/s,P,Q两点同时开始运动.设运动时间为T秒.