题目内容
12.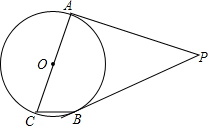 如图:PA、PB是⊙O的切线,切点为A、B,AC是直径,若∠P=50°,则∠ACB=65°.
如图:PA、PB是⊙O的切线,切点为A、B,AC是直径,若∠P=50°,则∠ACB=65°.
分析 连接BC,OB,由PA、PB是⊙O的切线,可得∠OAP=∠OBP=90°,根据四边形内角和,求出∠AOB,再根据圆周角定理即可求∠ACB的度数.
解答 解:连接BC,OB.
∵PA、PB是⊙O的切线,A、B为切点,
∴∠OAP=∠OBP=90°.
∴∠AOB=180°-∠P=130°,
由圆周角定理知,∠ACB=$\frac{1}{2}$∠AOB=65°,
故答案为:65.
点评 本题主要考查的是切线的性质,解决本题的关键是连接BC、OB,利用直径对的圆周角是直角,切线的性质,圆周角定理解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
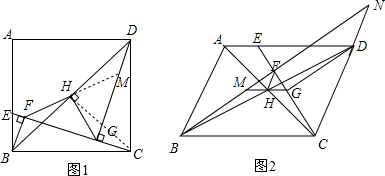
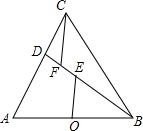 如图,在等边△ABC中,点D为AC边上一点连接BD,点O边AB中点,在BD上取点E,连接OE,使∠OEB=60°,过C作CF∥OE,CF交BD于F.求证:BF=2OE.
如图,在等边△ABC中,点D为AC边上一点连接BD,点O边AB中点,在BD上取点E,连接OE,使∠OEB=60°,过C作CF∥OE,CF交BD于F.求证:BF=2OE.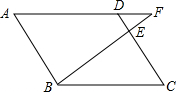 如图,在边长为4的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为$\frac{4}{3}$.
如图,在边长为4的菱形ABCD中,点E在边CD上,点F为BE延长线与AD延长线的交点.若DE=1,则DF的长为$\frac{4}{3}$. 如图所示,已知∠1=∠2,∠3=∠4.求证:AB=AC.
如图所示,已知∠1=∠2,∠3=∠4.求证:AB=AC. 如图,长方体的长、宽、高分别是4,3,5,现有绳子从A出发,沿长方形表面到达C处,问绳子最短是$\sqrt{74}$.
如图,长方体的长、宽、高分别是4,3,5,现有绳子从A出发,沿长方形表面到达C处,问绳子最短是$\sqrt{74}$.