题目内容
11.在△ABC中,点I是内心,∠BIC=114°,则∠A的度数为( )| A. | 57° | B. | 66° | C. | 48° | D. | 78° |
分析 在△BCI中求得∠IBC+∠ICB=66°,由切线长定理可知∠ABI=∠CBT、∠ACI=∠BCI,从而可求得∠ABC+∠ACB=132°,然后由三角形的内角和定理可求得∠A的度数.
解答 解:如图所示:
∵∠BIC=114°,
∴∠IBC+∠ICB=66°.
∵BC、BA为圆的切线,
∴∠ABI=∠CBT.
同理:∠ACI=∠BCI.
∴∠ABC+∠ACB=132°.
∴∠A=180°-∠ABC+∠ACB=180°-132°=48°.
故选:C.
点评 本题主要考查的是三角形的内切圆的性质、三角形的内角和定理,求得∠ABC+∠ACB=132°是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 △ABC中,∠ABC=120°,以AC为边向形外作等边三角形ACD,求证:BD=AB+BC.
△ABC中,∠ABC=120°,以AC为边向形外作等边三角形ACD,求证:BD=AB+BC.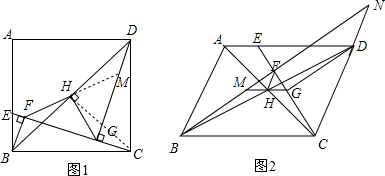
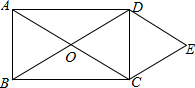 如图,在矩形ABCD中,对角线AC与BD交于点O,E是矩形ABCD外一点,且∠EDC=∠OCD,∠ECD=∠ODC,请说明CE=OA.
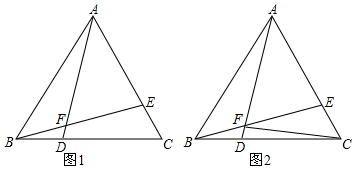
如图,在矩形ABCD中,对角线AC与BD交于点O,E是矩形ABCD外一点,且∠EDC=∠OCD,∠ECD=∠ODC,请说明CE=OA.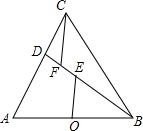 如图,在等边△ABC中,点D为AC边上一点连接BD,点O边AB中点,在BD上取点E,连接OE,使∠OEB=60°,过C作CF∥OE,CF交BD于F.求证:BF=2OE.
如图,在等边△ABC中,点D为AC边上一点连接BD,点O边AB中点,在BD上取点E,连接OE,使∠OEB=60°,过C作CF∥OE,CF交BD于F.求证:BF=2OE. 如图所示,已知∠1=∠2,∠3=∠4.求证:AB=AC.
如图所示,已知∠1=∠2,∠3=∠4.求证:AB=AC.