题目内容
如图，∠A＝∠B＝90°，E是AB上一点，且AE＝BC，∠1＝∠2.求证：△ADE≌△BEC.
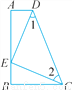
证明见解析
【解析】试题分析：由∠1=∠2，可得DE=CD，根据证明直角三角形全等的“HL”定理，证明即可.
试题解析：∵∠1＝∠2，
∴DE＝EC.
又∵∠A＝∠B＝90°，AE＝BC，
∴Rt△ADE≌Rt△BEC(HL).
练习册系列答案
名校课堂系列答案
相关题目
在△ABC中，已知AC=3，BC=4，AB=5，那么下列结论正确的是( )
A.sinA=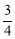
B.cosA=
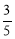C.tanA= 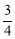D.cosB=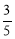
B
【解析】
试题分析：先根据勾股定理的逆定理判断△ABC的形状，再根据三角函数的定义依次分析各项即可.
∵
∴△ABC是直角三角形
∴，，，
故选B. 分解因式：2ab2－6a2b＋ab;
ab(2b－6a＋1)
【解析】试题分析：根据提公因式法分解因式，先确定公因式ab，再提取公因式即可.
试题解析：2ab2－6a2b＋ab = ab(2b－6a＋1). 如图所示，将Rt△ABC沿直角边AB的方向向右平移2个单位得到△DEF，如果AB＝4，∠ABC＝90°，且△ABC的面积为6，试求图中阴影部分的面积．
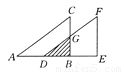
【解析】试题分析：根据△ABC的面积求出BC的长，根据平移的性质计算出BD的长，再根据平行线分线段成比例定理求出BG的长，最后利用三角形的面积公式计算即可得出答案．
试题解析：
【解析】
因为S△ABC＝AB·BC＝6，
所以BC＝3，
由平移可知AD＝2，BC∥EF，
所以BD＝AB－AD＝4－2＝2，
所以＝，
所以BG＝BC＝，
所以S△BD... 一个三角形最初的一个顶点为A，把它先向下平移4个单位长度时的位置记为B，再向左平移3个单位长度时的位置记为C，则由A，B，C三点所组成的三角形的周长为 ( )
A. 7 B. 14 C. 12 D. 15
C
【解析】试题分析：如图所示：
AB＝4，BC＝3，
则AC＝5，
故由A，B，C三点所组成的三角形的周长为：3＋4＋5＝12．
故选C． 如图，在Rt△ABC中，AC⊥BC，CD⊥AB，∠1=∠2，有下列结论：（1）AC∥DE；（2）∠A=∠3；（3）∠B=∠1；（4）∠B与∠2互余；（5）∠A=∠2．其中正确的有 （填写所有正确的序号）．
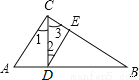
(1)、(2)、(3)
【解析】
试题分析：根据∠1=∠2，即内错角相等，两直线平行可得AC∥DE，则①正确；根据∠1+∠3=∠1+∠A=90°可得∠3=∠A，则②正确；根据∠1+∠3=∠3+∠B=90°可得∠B=∠1，则③正确；根据平行可得DE⊥BC，则∠3+∠2=∠B+∠3=90°，则∠2=∠B，则④错误；根据∠1=∠2，∠1≠∠A可得∠2≠∠A，则⑤错误. 如图所示，H是△ABC的高AD，BE的交点，且DH=DC，则下列结论：①BD=AD；②BC=AC；③BH=AC；④CE=CD中正确的有（ ）
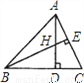
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】【解析】
①∵BE⊥AC，AD⊥BC，∴∠AEH=∠ADB=90°．
∵∠HBD+∠BHD=90°，∠EAH+∠AHE=90°，∠BHD=∠AHE，∴∠HBD=∠EAH．
∵DH=DC，∴△BDH≌△ADC（AAS），∴BD=AD，BH=AC；
②∵BC=AC，∴∠BAC=∠ABC．
由①知，在Rt△ABD中，∵BD=AD，∴∠ABC=45°，∴∠BAC... 用反证法证明命题“三角形中至少有一个内角大于或等于60°”，第一步应假设 。
三角形的三个内角都小于60°．
【解析】
试题分析：熟记反证法的步骤，直接填空即可．
试题解析：第一步应假设结论不成立，即三角形的三个内角都小于60°． 设a，b，c，d都是整数，且a＜2b，b＜3c，c＜4d，d＜20，则a的最大值是（ ）
A. 480 B. 479 C. 448 D. 447
D
【解析】由a，b，c，d都是整数，且a＜2b，b＜3c，c＜4d，d＜20，可知d=19，c＜4×19=76，代入可得c=75，b＜3×75=225，再次代入b=224，a＜2×224=448，因此可求出a=447，
故选：D．