题目内容
图形平移的主要因素是移动的________________
 方向和距离
【解析】试题解析:图形的平移主要有两个方面决定即方向和距离.
故答案为:方向和距离.
方向和距离
【解析】试题解析:图形的平移主要有两个方面决定即方向和距离.
故答案为:方向和距离.
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
分解因式:2ab2-6a2b+ab;
 ab(2b-6a+1)
【解析】试题分析:根据提公因式法分解因式,先确定公因式ab,再提取公因式即可.
试题解析:2ab2-6a2b+ab = ab(2b-6a+1).
ab(2b-6a+1)
【解析】试题分析:根据提公因式法分解因式,先确定公因式ab,再提取公因式即可.
试题解析:2ab2-6a2b+ab = ab(2b-6a+1). 如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )
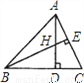
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】【解析】
①∵BE⊥AC,AD⊥BC,∴∠AEH=∠ADB=90°.
∵∠HBD+∠BHD=90°,∠EAH+∠AHE=90°,∠BHD=∠AHE,∴∠HBD=∠EAH.
∵DH=DC,∴△BDH≌△ADC(AAS),∴BD=AD,BH=AC;
②∵BC=AC,∴∠BAC=∠ABC.
由①知,在Rt△ABD中,∵BD=AD,∴∠ABC=45°,∴∠BAC...
B
【解析】【解析】
①∵BE⊥AC,AD⊥BC,∴∠AEH=∠ADB=90°.
∵∠HBD+∠BHD=90°,∠EAH+∠AHE=90°,∠BHD=∠AHE,∴∠HBD=∠EAH.
∵DH=DC,∴△BDH≌△ADC(AAS),∴BD=AD,BH=AC;
②∵BC=AC,∴∠BAC=∠ABC.
由①知,在Rt△ABD中,∵BD=AD,∴∠ABC=45°,∴∠BAC... 用反证法证明命题“三角形中至少有一个内角大于或等于60°”,第一步应假设 。
 三角形的三个内角都小于60°.
【解析】
试题分析:熟记反证法的步骤,直接填空即可.
试题解析:第一步应假设结论不成立,即三角形的三个内角都小于60°.
三角形的三个内角都小于60°.
【解析】
试题分析:熟记反证法的步骤,直接填空即可.
试题解析:第一步应假设结论不成立,即三角形的三个内角都小于60°. 图形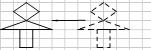 左边的图形是由右边的图形怎样平移得到的?
左边的图形是由右边的图形怎样平移得到的?
 向左平移6个单位.
【解析】试题分析:观察图形中对应点的变化,即可得出图形的变化规律.
试题解析:
根据题意可以得到左边的图形是由右边的图形向左平移6个单位长度平移得到的.
向左平移6个单位.
【解析】试题分析:观察图形中对应点的变化,即可得出图形的变化规律.
试题解析:
根据题意可以得到左边的图形是由右边的图形向左平移6个单位长度平移得到的. 平移前后两个图形__________
 全等
【解析】试题解析:图形平移前后两个图形是全等的.
故答案为:全等.
全等
【解析】试题解析:图形平移前后两个图形是全等的.
故答案为:全等. 下列图形经过平移后恰好可以与原图形组合成一个长方形的是( )
A. 三角形 B. 正方形 C. 梯形 D. 都有可能
 B
【解析】试题解析:正方形能够通过平移而得到的新图形和原图形组合成一个长方形.
故选B.
B
【解析】试题解析:正方形能够通过平移而得到的新图形和原图形组合成一个长方形.
故选B. 设a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,则a的最大值是( )
A. 480 B. 479 C. 448 D. 447
 D
【解析】由a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,可知d=19,c<4×19=76,代入可得c=75,b<3×75=225,再次代入b=224,a<2×224=448,因此可求出a=447,
故选:D.
D
【解析】由a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,可知d=19,c<4×19=76,代入可得c=75,b<3×75=225,再次代入b=224,a<2×224=448,因此可求出a=447,
故选:D. 下列哪个多项式能分解成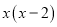 ( )
( )
A. 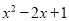 B.
B. 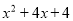 C.
C. 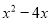 D.
D. 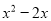
 D
【解析】利用因式分解是整式乘法的逆运算,可知x(x-2)=.
故选:D.
D
【解析】利用因式分解是整式乘法的逆运算,可知x(x-2)=.
故选:D. 
