题目内容
19992+1999能被2000整除吗?
 能
【解析】试题分析:根据提公因式法--因式分解,化为几个因数积的形式,而得到整除的结论.
试题解析:因为19992+1999=1999×(1999+1)=1999×2000,
所以19992+1999能被1999整除,也能被2000整除.
能
【解析】试题分析:根据提公因式法--因式分解,化为几个因数积的形式,而得到整除的结论.
试题解析:因为19992+1999=1999×(1999+1)=1999×2000,
所以19992+1999能被1999整除,也能被2000整除.
练习册系列答案
相关题目
用反证法证明命题“三角形中至少有一个内角大于或等于60°”,第一步应假设 。
 三角形的三个内角都小于60°.
【解析】
试题分析:熟记反证法的步骤,直接填空即可.
试题解析:第一步应假设结论不成立,即三角形的三个内角都小于60°.
三角形的三个内角都小于60°.
【解析】
试题分析:熟记反证法的步骤,直接填空即可.
试题解析:第一步应假设结论不成立,即三角形的三个内角都小于60°. 设a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,则a的最大值是( )
A. 480 B. 479 C. 448 D. 447
 D
【解析】由a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,可知d=19,c<4×19=76,代入可得c=75,b<3×75=225,再次代入b=224,a<2×224=448,因此可求出a=447,
故选:D.
D
【解析】由a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,可知d=19,c<4×19=76,代入可得c=75,b<3×75=225,再次代入b=224,a<2×224=448,因此可求出a=447,
故选:D. 如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是__________.
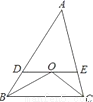
 9
【解析】∵在△ABC中,∠B与∠C的平分线交于点O,
∴∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,
∴OD=BD,OE=CE,
∵AB=5,AC=4,
∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+A...
9
【解析】∵在△ABC中,∠B与∠C的平分线交于点O,
∴∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,
∴OD=BD,OE=CE,
∵AB=5,AC=4,
∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+A... 下面命题不正确的是( )
A. 两个内角分别是50°和65°的三角形是等腰三角形
B. 两个外角相等的三角形是等腰三角形
C. 一个外角的平分线平行于一边的三角形是等腰三角形
D. 两个内角不相等的三角形不是等腰三角形
 D
【解析】解:A.第三个角180°﹣50°﹣65°=65°,有两角相等的三角形是等腰三角形,正确;
B.外角相等,则对应的内角也相等,有两角相等的三角形是等腰三角形,正确;
C.利用两直线平行,内错角相等,同位相等,可知,另外的两内角也相等,有两角相等的三角形是等腰三角形,正确;
D.两个内角不相等的三角形可能是等腰三角形,错误.
故选D.
D
【解析】解:A.第三个角180°﹣50°﹣65°=65°,有两角相等的三角形是等腰三角形,正确;
B.外角相等,则对应的内角也相等,有两角相等的三角形是等腰三角形,正确;
C.利用两直线平行,内错角相等,同位相等,可知,另外的两内角也相等,有两角相等的三角形是等腰三角形,正确;
D.两个内角不相等的三角形可能是等腰三角形,错误.
故选D. 多项式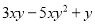 的公因式是__________
的公因式是__________
 y
【解析】根据提公因式的方法:一看系数、二看字母(相同的字母或因式,次数最低),可得公因式为y.
故答案为:y.
y
【解析】根据提公因式的方法:一看系数、二看字母(相同的字母或因式,次数最低),可得公因式为y.
故答案为:y. 下列哪个多项式能分解成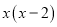 ( )
( )
A. 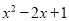 B.
B. 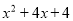 C.
C. 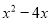 D.
D. 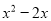
 D
【解析】利用因式分解是整式乘法的逆运算,可知x(x-2)=.
故选:D.
D
【解析】利用因式分解是整式乘法的逆运算,可知x(x-2)=.
故选:D. 若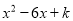 是一个完全平方式,那么k=_______________
是一个完全平方式,那么k=_______________
 9
【解析】因为若是一个完全平方式,那么,那么答案是k=9.
故答案为:9.
9
【解析】因为若是一个完全平方式,那么,那么答案是k=9.
故答案为:9. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
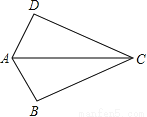
A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
 C
【解析】试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能. A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC...
C
【解析】试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能. A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC... 
