题目内容
5.如图a是长方形纸带,∠DEF=24°,第一次操作:将纸带沿EF折叠成图b,第二次操作:沿BF折叠成图c,第三次操作:将纸带沿EF折叠,第四次操作:沿BF折叠…则第五次操作中的∠CFE的度数是( )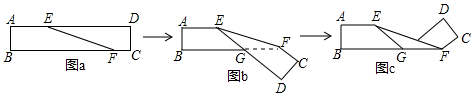
| A. | 108° | B. | 84° | C. | 60° | D. | 36° |
分析 根据两条直线平行,内错角相等,则∠BFE=∠DEF=24°,根据平角定义,则∠EFC=156°(图a),进一步求得∠BFC=156°-24°=132°(图b),依此类推,即可得出答案.
解答 解:∵AD∥BC,∠DEF=24°,
∴∠BFE=∠DEF=24°,
∴∠EFC=156°(图a),
∴∠BFC=156°-24°=132°(图b),(1次)
∴∠CFE=132°-24°=108°(图c). (2次)
依此类推:108°-24°=84° (3次)
84°-24°=60°,(4次)
60°-24°=36°,(5次);
故选:D.
点评 此题主要考查了翻折变换的性质,根据折叠能够发现相等的角进而求出是解题关键.

练习册系列答案
相关题目
16.如图,是某几何体的三视图及相关数据,则该几何体的表面积是( )


| A. | 39π | B. | 29π | C. | 24π | D. | 19π |
20.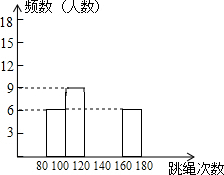 某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
请结合图表解答下列问题:
(1)表中的m=12;
(2)请把频数分布直方图补完整;
(3)这个样本数据的中位数落在第三组;
(4)若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.
 某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.| 组别 | 次数x | 频数(人数) |
| A | 80≤x<100 | 6 |
| B | 100≤x<120 | 8 |
| C | 120≤x<140 | m |
| D | 140≤x<160 | 18 |
| E | 160≤x<180 | 6 |
(1)表中的m=12;
(2)请把频数分布直方图补完整;
(3)这个样本数据的中位数落在第三组;
(4)若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.
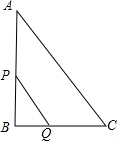 如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.
如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s. 如图,已知一次函数y1=$\frac{4}{3}$x-4与反比例函数y2=$\frac{k}{x}$的图象在第一象限相交于点A(6,n),与x轴相交于点B.
如图,已知一次函数y1=$\frac{4}{3}$x-4与反比例函数y2=$\frac{k}{x}$的图象在第一象限相交于点A(6,n),与x轴相交于点B.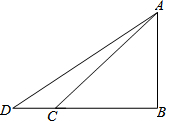 如图,要测量旗杆AB的高度,在地面C点处测得旗杆顶部A点的仰角为45°,从C点向外走2米到D点处,(B、C、D三点在同一直线上)测得旗杆顶部A点的仰角为37°,求旗杆AB的高度.
如图,要测量旗杆AB的高度,在地面C点处测得旗杆顶部A点的仰角为45°,从C点向外走2米到D点处,(B、C、D三点在同一直线上)测得旗杆顶部A点的仰角为37°,求旗杆AB的高度.