题目内容
15.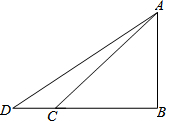 如图,要测量旗杆AB的高度,在地面C点处测得旗杆顶部A点的仰角为45°,从C点向外走2米到D点处,(B、C、D三点在同一直线上)测得旗杆顶部A点的仰角为37°,求旗杆AB的高度.
如图,要测量旗杆AB的高度,在地面C点处测得旗杆顶部A点的仰角为45°,从C点向外走2米到D点处,(B、C、D三点在同一直线上)测得旗杆顶部A点的仰角为37°,求旗杆AB的高度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
分析 在Rt△ABC中利用∠ABC=90°,∠ACB=45°可知AB=BC,设AB=x米,则BD=(x+2)米,在Rt△ABD中,利用锐角三角函数的定义即可得出x的值.
解答 解:在Rt△ABC中,
∵∠ABC=90°,∠ACB=45°.
∴AB=BC.
设AB=x米,则BD=(x+2)米,
在Rt△ABD中,
∵∠ABD=90°,∠ADB=37°
∴tan∠D=$\frac{AB}{BD}$,即0.75=$\frac{x}{x+2}$,解得x=6.
答:旗杆AB的高度为6米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.

练习册系列答案
相关题目
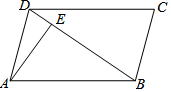 如图,在?ABCD中,DB=DC,∠C的度数比∠ABD的度数大54°,AE⊥BD于点E,则∠DAE的度数等于12°.
如图,在?ABCD中,DB=DC,∠C的度数比∠ABD的度数大54°,AE⊥BD于点E,则∠DAE的度数等于12°.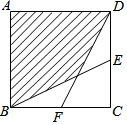 如图,正方形ABCD的边长为2cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是$\frac{8}{3}$cm2.
如图,正方形ABCD的边长为2cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是$\frac{8}{3}$cm2. 在平行四边形ABCD中,AB=2AD.
在平行四边形ABCD中,AB=2AD.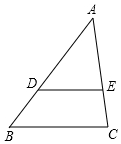 如图,在△ABC中,DE∥BC,AD=2BD,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$-\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.
如图,在△ABC中,DE∥BC,AD=2BD,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$-\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.