题目内容
10.在平面直角坐标系中,点A、B的坐标分别为(-3,0)、(3,0),点P在反比例函数y=$\frac{9}{x}$的图象上.若△PAB为直角三角形,则满足条件的点P的个数为( )| A. | 2个 | B. | 4个 | C. | 5个 | D. | 6个 |
分析 设点P的坐标为(x,y),分∠APB=90°、∠PAB=90°和∠PBA=90°三种情况考虑:当∠APB=90°时,以AB为直径作圆,由圆与双曲线无交点可知此时点P不存在;当∠PAB=90°时,可找出x=-3,进而可得出点P的坐标;当∠PBA=90°时,可找出x=3,进而可得出点P的坐标.综上即可得出结论.
解答 解:设点P的坐标为(x,y),
当∠APB=90°时,以AB为直径作圆,如图所示,
∵圆与双曲线无交点,
∴点P不存在;
当∠PAB=90°时,x=-3,
y=$\frac{9}{x}$=-3,
∴点P的坐标(-3,-3);
当∠PBA=90°时,x=3,
y=$\frac{9}{x}$=3,
∴点P的坐标为(3,3).
综上所述:满足条件的点P有2个.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征以及直角三角形,依照题意画出图形,利用数形结合解决问题是解题的关键.

练习册系列答案
相关题目
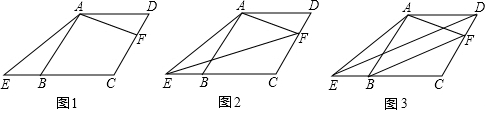
 如图,在?ABCD中,DB=DC,∠C=58°,AE⊥BD于E,则∠DAE=32度.
如图,在?ABCD中,DB=DC,∠C=58°,AE⊥BD于E,则∠DAE=32度.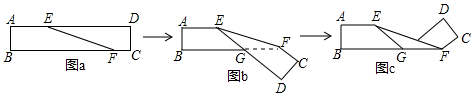
 在平行四边形ABCD中,AB=2AD.
在平行四边形ABCD中,AB=2AD.