��Ŀ����
14��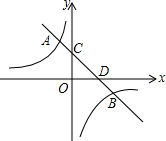 ��ͼ������������y=$\frac{k}{x}$��һ�κ���y=kx-k+2��ͬһֱ������ϵ�е�ͼ���ཻ��A��B���㣬����A��-1��3����ֱ��y=kx-k+2��������ֱ���C��D���㣬����˵������k��0���ڵ�B������Ϊ��3��-1�����۵�x��-1ʱ��$\frac{k}{x}$��kx-k+2����tan��OCD=-$\frac{1}{k}$��������ȷ���ǣ�������
��ͼ������������y=$\frac{k}{x}$��һ�κ���y=kx-k+2��ͬһֱ������ϵ�е�ͼ���ཻ��A��B���㣬����A��-1��3����ֱ��y=kx-k+2��������ֱ���C��D���㣬����˵������k��0���ڵ�B������Ϊ��3��-1�����۵�x��-1ʱ��$\frac{k}{x}$��kx-k+2����tan��OCD=-$\frac{1}{k}$��������ȷ���ǣ�������| A�� | �٢� | B�� | �٢ڢ� | C�� | �٢ۢ� | D�� | �٢ڢۢ� |
���� ���ݷ�����������һ�κ�����ͼ��ó��������꣬�ٽ��з����жϼ��ɣ�
��� �⣺�߷���������y=$\frac{k}{x}$��һ�κ���y=kx-k+2��ͼ����A��-1��3����
��3=$\frac{k}{-1}$��3=-k-k+2��
��k=-3��k=-$\frac{1}{2}$��
��k��0��ȷ��
�߷���������y=$\frac{-3}{x}$��һ�κ���y=-$\frac{1}{2}$x+$\frac{5}{2}$��ͬһֱ������ϵ�е�ͼ���ཻ��A��B���㣬
�ɵõ�B������Ϊ��6��-$\frac{1}{2}$����
��ڵ�B������Ϊ��3��-1������
����ͼ��ɵã���x��-1ʱ��$\frac{k}{x}$��kx-k+2����ȷ��
��tan��OCD=$\frac{OD}{OC}$=$\frac{-\frac{-k+2}{k}}{-k+2}=-\frac{1}{k}$����ȷ��
��ѡC��
���� ���⿼�鷴����������һ�κ����Ľ��㣬�ؼ������ô���ϵ�����ó�����������������

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
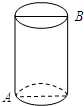 ��ͼ��ʾ����һ��Բ���壬��Ϊ12cm������뾶Ϊ3cm����Բ���µ���A����һֻ֩�룮���뵽�ϵ���B��סһֻ��Ӭ����֩�����ߵ����·�߳�ӦΪ6$\sqrt{5}$cm����ȡ3.0����
��ͼ��ʾ����һ��Բ���壬��Ϊ12cm������뾶Ϊ3cm����Բ���µ���A����һֻ֩�룮���뵽�ϵ���B��סһֻ��Ӭ����֩�����ߵ����·�߳�ӦΪ6$\sqrt{5}$cm����ȡ3.0����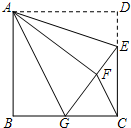 ��ͼ��������ABCD�У�CD=6����E�ڱ�CD�ϣ���CD=3DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF��
��ͼ��������ABCD�У�CD=6����E�ڱ�CD�ϣ���CD=3DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF��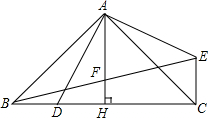 ��֪��AC=AB��AD=AE��AD��AE��AB��AC�������Ϊ��A������BE��AH��BC������Ϊ��H��AH��BE�ཻ��F����֤��BF=EF��
��֪��AC=AB��AD=AE��AD��AE��AB��AC�������Ϊ��A������BE��AH��BC������Ϊ��H��AH��BE�ཻ��F����֤��BF=EF��