题目内容
4.化简并求值:$\frac{2a}{{{a^2}-{b^2}}}-\frac{1}{a+b}$.其中:a=$\sqrt{8}$,b=$\sqrt{2}$.分析 原式通分并利用同分母分式的减法法则计算,约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:原式=$\frac{2a}{(a+b)(a-b)}$-$\frac{a-b}{(a+b)(a-b)}$=$\frac{a+b}{(a+b)(a-b)}$=$\frac{1}{a-b}$,
当a=$\sqrt{8}$=2$\sqrt{2}$,b=$\sqrt{2}$时,原式=$\frac{\sqrt{2}}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.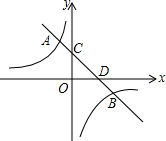 如图,反比例函数y=$\frac{k}{x}$与一次函数y=kx-k+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=kx-k+2与坐标轴分别交于C,D两点,下列说法:①k<0;②点B的坐标为(3,-1);③当x<-1时,$\frac{k}{x}$<kx-k+2;④tan∠OCD=-$\frac{1}{k}$,其中正确的是( )
如图,反比例函数y=$\frac{k}{x}$与一次函数y=kx-k+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=kx-k+2与坐标轴分别交于C,D两点,下列说法:①k<0;②点B的坐标为(3,-1);③当x<-1时,$\frac{k}{x}$<kx-k+2;④tan∠OCD=-$\frac{1}{k}$,其中正确的是( )
 如图,反比例函数y=$\frac{k}{x}$与一次函数y=kx-k+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=kx-k+2与坐标轴分别交于C,D两点,下列说法:①k<0;②点B的坐标为(3,-1);③当x<-1时,$\frac{k}{x}$<kx-k+2;④tan∠OCD=-$\frac{1}{k}$,其中正确的是( )
如图,反比例函数y=$\frac{k}{x}$与一次函数y=kx-k+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=kx-k+2与坐标轴分别交于C,D两点,下列说法:①k<0;②点B的坐标为(3,-1);③当x<-1时,$\frac{k}{x}$<kx-k+2;④tan∠OCD=-$\frac{1}{k}$,其中正确的是( )| A. | ①③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
9.对某条路线的长度进行5次测量,得到5个结果(单位:km):x1=104,x2=101,x3=102,x4=104,x5=103.如果用x作为这条路线长度的近似值,要使得(x-x1)2+(x-x2)2+…+(x-x5)2的值最小,x应选取这5次测量结果的( )
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 最小值 |
16.2015的相反数是( )
| A. | 2015 | B. | -2015 | C. | -$\frac{1}{2015}$ | D. | $\frac{1}{2015}$ |
11.若$\frac{a}{b}$=$\frac{2}{5}$,则$\frac{a+b}{b}$=( )
| A. | $\frac{7}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{7}$ |
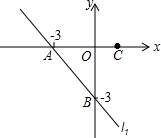 如图,在平面直角坐标系中,直线l1分别与x轴、y轴分别交于A、B两点,与抛物线y=x2+bx+c经过点A、B,且抛物线的对称轴为直线x=-1且过C点(点C点A的右侧).
如图,在平面直角坐标系中,直线l1分别与x轴、y轴分别交于A、B两点,与抛物线y=x2+bx+c经过点A、B,且抛物线的对称轴为直线x=-1且过C点(点C点A的右侧).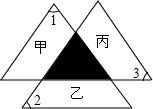 如图的灰色小三角形为三个全等大三角形的重迭处,且三个大三角形各扣掉灰色小三角形后分别为甲、乙、丙三个梯形.若图中标示的∠1为58°,∠2为62°,∠3为60°,则关于甲、乙、丙三梯形的高的大小关系,下列叙述何者正确?( )
如图的灰色小三角形为三个全等大三角形的重迭处,且三个大三角形各扣掉灰色小三角形后分别为甲、乙、丙三个梯形.若图中标示的∠1为58°,∠2为62°,∠3为60°,则关于甲、乙、丙三梯形的高的大小关系,下列叙述何者正确?( )