题目内容
19.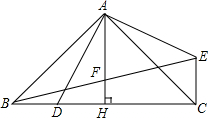 已知:AC=AB,AD=AE,AD⊥AE,AB⊥AC,垂足均为点A,连接BE,AH⊥BC,垂足为点H,AH与BE相交于F.求证:BF=EF.
已知:AC=AB,AD=AE,AD⊥AE,AB⊥AC,垂足均为点A,连接BE,AH⊥BC,垂足为点H,AH与BE相交于F.求证:BF=EF.
分析 先求出∠BAD=∠CAE,证明△ABD≌△ACE,得出∠ABD=∠ACE=45°,求出∠BCE=90°,证出AH∥CE,由等腰三角形的三线合一性质得出BH=CH,证出FH是△BCE的中位线,即可得出结论.
解答 证明:∵AD⊥AE,AB⊥AC,AC=AB,
∴∠DAE=∠BAC=90°,∠ABC=∠ACB=45°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠BAD=∠CAE}&{\;}\\{AD=AE}&{\;}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE=45°,
∴∠BCE=45°+45°=90°,
∴CE⊥BC,
∵AH⊥BC,
∴AH∥CE,BH=CH,
∴FH是△BCE的中位线,
∴BF=EF.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质、三角形中位线定理;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
9.学校春游,如果每辆汽车坐45人,则有28人没有上车;如果每辆坐50人,则空出一辆汽车,并且有一辆车还可以坐12人,设有x辆汽车,可列方程( )
| A. | 45x-28=50(x-1)-12 | B. | 45x+28=50(x-1)+12 | C. | 45x+28=50(x-1)-12 | D. | 45x-28=50(x-1)+12 |
10.已知:2m=1,2n=3,则2m+2n=( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
14.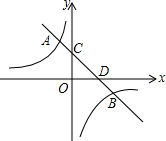 如图,反比例函数y=$\frac{k}{x}$与一次函数y=kx-k+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=kx-k+2与坐标轴分别交于C,D两点,下列说法:①k<0;②点B的坐标为(3,-1);③当x<-1时,$\frac{k}{x}$<kx-k+2;④tan∠OCD=-$\frac{1}{k}$,其中正确的是( )
如图,反比例函数y=$\frac{k}{x}$与一次函数y=kx-k+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=kx-k+2与坐标轴分别交于C,D两点,下列说法:①k<0;②点B的坐标为(3,-1);③当x<-1时,$\frac{k}{x}$<kx-k+2;④tan∠OCD=-$\frac{1}{k}$,其中正确的是( )
 如图,反比例函数y=$\frac{k}{x}$与一次函数y=kx-k+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=kx-k+2与坐标轴分别交于C,D两点,下列说法:①k<0;②点B的坐标为(3,-1);③当x<-1时,$\frac{k}{x}$<kx-k+2;④tan∠OCD=-$\frac{1}{k}$,其中正确的是( )
如图,反比例函数y=$\frac{k}{x}$与一次函数y=kx-k+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=kx-k+2与坐标轴分别交于C,D两点,下列说法:①k<0;②点B的坐标为(3,-1);③当x<-1时,$\frac{k}{x}$<kx-k+2;④tan∠OCD=-$\frac{1}{k}$,其中正确的是( )| A. | ①③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
8.李克强总理在2015年3月5日的《政府工作报告》中表示,2015年铁路将投资8000亿元.将8000亿元用科学记数法表示为( )
| A. | 8×1011元 | B. | 80×1010元 | C. | 8000×108元 | D. | 8×103元 |
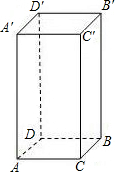 如图,已知长方体的长2cm、宽为1cm、高为4cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是5cm.
如图,已知长方体的长2cm、宽为1cm、高为4cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是5cm.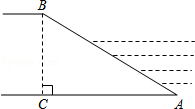 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,求坡面AB的长.
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,求坡面AB的长.