题目内容
3.已知△ABC三边a,b,c满足(a-c):(a+b):(c-b)=-2:7:1,且a+b+c=24cm.(1)求a,b,c的值;
(2)判断△ABC的形状.
分析 (1)设a-c=-2k,a+b=7k,c-b=k,于是得到a=7k-b,c=k+b,代入a-c=-2k和a+b+c=24,解$\left\{\begin{array}{l}{8k-2b=0}\\{8k+b=24}\end{array}\right.$,得到k=2,b=8,求得a=6,c=10即可;
(2)根据勾股定理的逆定理即可判断△ABC的形状.
解答 解:(1)设a-c=-2k,a+b=7k,c-b=k,
∴a=7k-b,c=k+b,
∴a-c=7k-b-k-b=-2k,
∵a+b+c=24,
∴7k-b+b+k+b=24,
∴$\left\{\begin{array}{l}{8k-2b=0}\\{8k+b=24}\end{array}\right.$,
解得:k=2,b=8,
∴a=6,c=10;
(2)∵a2+b2=62+82=100=102=c2,
∴△ABC是直角三角形.
点评 本题考查了比例线段,勾股定理的逆定理,熟练掌握比例线段的性质是解题的关键.

练习册系列答案
相关题目
14.下列描述不属于定义的是( )
| A. | 两组对边分别平行的四边形叫做平行四边形 | |
| B. | 正三角形是特殊的等腰三角形 | |
| C. | 在同一平面内三条线段首尾顺次连接得到的图形叫做三角形 | |
| D. | 含有未知数的等式叫做方程 |
 如图,矩形ABCD沿AE折叠,使点D落在BC边上的F点处,AD=5,AB=4,求CE的长.
如图,矩形ABCD沿AE折叠,使点D落在BC边上的F点处,AD=5,AB=4,求CE的长. 如图所示,△ABC∽△ACD,且AD=5,BD=4,求△ACD与△ABC的相似比.
如图所示,△ABC∽△ACD,且AD=5,BD=4,求△ACD与△ABC的相似比.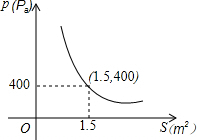 某校科技小组进行野外考察,途中遇到一片十几米宽的湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺若干块木板,构筑成一条临时通道,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当木板压强不超过6 000Pa时,木板的面积至少应为0.1m2.
某校科技小组进行野外考察,途中遇到一片十几米宽的湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺若干块木板,构筑成一条临时通道,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当木板压强不超过6 000Pa时,木板的面积至少应为0.1m2.