题目内容
7.计算:(1)$\frac{2a}{5{a}^{2}b}+\frac{3b}{10a{b}^{2}}$;
(2)$\frac{3y}{2x+2y}+\frac{2xy}{{x}^{2}+xy}$;
(3)a-b+$\frac{{b}^{2}}{a+b}$;
(4)$\frac{2x}{{x}^{2}-64{y}^{2}}$-$\frac{1}{x-8y}$;
(5)$\frac{b}{a}$-$\frac{a}{b}$-$\frac{{a}^{2}+{b}^{2}}{ab}$;
(6)$\frac{2m}{5{n}^{2}p}$-$\frac{3n}{4m{p}^{2}}$.
分析 原式各项通分并利用同分母分式的加减法则计算即可得到结果.
解答 解:(1)原式=$\frac{4ab+3ab}{10{a}^{2}{b}^{2}}$=$\frac{7ab}{10{a}^{2}{b}^{2}}$=$\frac{7}{10ab}$;
(2)原式=$\frac{3xy+4xy}{2x(x+y)}$=$\frac{7y}{2(x+y)}$;
(3)原式=$\frac{{a}^{2}-{b}^{2}+{b}^{2}}{a+b}$=$\frac{{a}^{2}}{a+b}$;
(4)原式=$\frac{2x-x-8y}{(x+8y)(x-8y)}$=$\frac{1}{x+8y}$;
(5)原式=$\frac{{b}^{2}-{a}^{2}-{a}^{2}-{b}^{2}}{ab}$=-$\frac{2a}{b}$;
(6)原式=$\frac{8{m}^{2}p-15{n}^{3}}{20m{n}^{2}{p}^{2}}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.如果4a2+1与一个单项式的和恰好是一个整式的平方,那么这样的单项式共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 5个 |
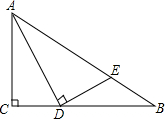 如图,在Rt△ABC中,∠C=90°,点D在边BC上,过点D作DE⊥AD交AB于点E,且DE=BE.
如图,在Rt△ABC中,∠C=90°,点D在边BC上,过点D作DE⊥AD交AB于点E,且DE=BE. 一个无盖长方体盒子的容积是V.
一个无盖长方体盒子的容积是V. 如图,半径为5的⊙O中,OD⊥AB,连接AD,AD=2$\sqrt{5}$,则AB=8.
如图,半径为5的⊙O中,OD⊥AB,连接AD,AD=2$\sqrt{5}$,则AB=8.