题目内容
17. 如图,半径为5的⊙O中,OD⊥AB,连接AD,AD=2$\sqrt{5}$,则AB=8.
如图,半径为5的⊙O中,OD⊥AB,连接AD,AD=2$\sqrt{5}$,则AB=8.
分析 设AC=x,CD=y,则OC=5-y,在Rt△ACD与Rt△AOC中根据勾股定理求出y的值,进而得出x的值即可.
解答 解:设AC=x,CD=y,则OC=5-y,AB=2x,
在Rt△ACD中,
∵AD=2$\sqrt{5}$,AC2+CD2=AD2,
∴x2+y2=(2$\sqrt{5}$)2①,
在Rt△AOC中,
∵OA=5,OC2+AC2=OA2,
∴(5-y)2+x2=52②,
①-②得,y=2,x=4,
∴AB=2x=8.
故答案为:8.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
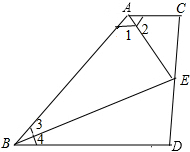 如图,AD∥BC,∠1=∠2,E为CD的中点,求证:∠3=∠4.
如图,AD∥BC,∠1=∠2,E为CD的中点,求证:∠3=∠4. 在ABC中,AB=AC,∠BAC=120°,AB=4cm,∠1=∠2,求AD的长.
在ABC中,AB=AC,∠BAC=120°,AB=4cm,∠1=∠2,求AD的长.