题目内容
16.下列函数有最大值还是最小值?求出当x为何值时,y取得最大值或最小值,并求出最大值与最小值.(1)y=x2+x-1;
(2)y=-2x2-3x+5.
分析 (1)先根据a的值确定函数图象的开口方向,确定函数有最大值还是有最小值,再代入顶点坐标求出即可;
(2)先根据a的值确定函数图象的开口方向,确定函数有最大值还是有最小值,再代入顶点坐标求出即可.
解答 解:(1)y=x2+x-1,
∵a=1>0,函数的图象的开口向上,
∴函数有最小值,
当x=-$\frac{b}{2a}$=-$\frac{1}{2×1}$=-$\frac{1}{2}$时,y最小值=$\frac{4×1×(-1)-{1}^{2}}{4×1}$=-$\frac{5}{4}$;
(2)y=-2x2-3x+5,
∵a=-2<0,函数的图象的开口向下,
∴函数有最大值,
当x=-$\frac{b}{2a}$=-$\frac{-3}{2×(-2)}$=-$\frac{3}{4}$时,y最大值=$\frac{4×(-2)×5-(-3)^{2}}{4×(-2)}$=$\frac{49}{8}$.
点评 本题考查了函数的最值的应用,能理解函数的最值的求法是解此题的关键,注意:数形结合思想的应用.

练习册系列答案
相关题目
 如图,在正方形ABCD中,E、F分别为AB、CD的中点,将正方形的两个角折起,使得顶点A和B都重合于线段EF上的点G,求∠α的度数.
如图,在正方形ABCD中,E、F分别为AB、CD的中点,将正方形的两个角折起,使得顶点A和B都重合于线段EF上的点G,求∠α的度数.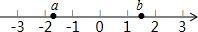 实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+2)^{2}}$+$\sqrt{(b-2)^{2}}$+$\sqrt{(a-b)^{2}}$.
实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+2)^{2}}$+$\sqrt{(b-2)^{2}}$+$\sqrt{(a-b)^{2}}$. 在ABC中,AB=AC,∠BAC=120°,AB=4cm,∠1=∠2,求AD的长.
在ABC中,AB=AC,∠BAC=120°,AB=4cm,∠1=∠2,求AD的长.