题目内容
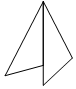
12. 如图所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列结论错误的是( )
如图所示,已知AC⊥BC于C,DE⊥AB于E,AD平分∠BAC,下列结论错误的是( )| A. | BD+DE=BC | B. | DE平分∠ADB | C. | AD平分∠EDC | D. | ED+AC>AD |
分析 根据角平分线上的点到角的两边的距离相等可得DE=DC,然后利用AAS证明△ACD≌△AED,再对各选项分析判断后利用排除法.
解答 解:∵AC⊥BC,DE⊥AB,AD平分∠BAC,
∴DE=DC,
A、BD+ED=BD+DC=BC,故本选项不符合题意;
B、C、在△ACD与△AED中,
$\left\{\begin{array}{l}{∠DAC=∠DAE}\\{∠ACD=∠AED=90°}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△AED(AAS),
∴∠ADC=∠ADE,
∴AD平分∠EDC,故C选项不符合题意;
但∠ADE与∠BDE不一定相等,故B选项符合题意;
D、∵△ACD≌△AED,
∴AE=AC,
∴ED+AC=ED+AE>AD(三角形任意两边之和大于第三边),故本选项不符合题意.
故选B.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,证明△ACD≌△AED是解题的关键.

练习册系列答案
相关题目
2.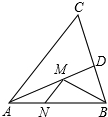 如图,在锐角△ABC中,AB=8,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,AB=8,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
 如图,在锐角△ABC中,AB=8,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,AB=8,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )| A. | 8 | B. | 6 | C. | $4\sqrt{2}$ | D. | $3\sqrt{2}$ |
20.下列各式计算正确的是( )
| A. | $\frac{a+c}{a+b}=\frac{c}{b}$ | B. | $\frac{a-c}{-a+b}=-\frac{a-c}{a+b}$ | ||
| C. | $\frac{x^8}{x^2}={x^4}$ | D. | $\frac{b}{{3{a^2}}}+\frac{1}{6ab}=\frac{{2{b^2}+a}}{{6{a^2}b}}$ |
2.若a<0,那么数a和它的相反数的差的绝对值等于( )
| A. | a | B. | 2a | C. | -a | D. | -2a |